Numpy et permet utilitzar matrius per realitzar càlculs de manera eficient.
On this page
- Què és i per a què serveix NumPy ?
- Creació d’arrays
- Tipus de dades de matrius de Numpy.
- Operacions amb valors de matrius.
- Còpies de matrius: view vs copy.
- Valors constants de numpy.
- Tractament valors no existents: NaN.
- Filtratge, edició i esborrat d’elements d’arrays.
- Operacions numèriques amb matrius
- Generar números aleatoris
- Operacions estadístiques amb matrius
- Com aconseguir valors únics.
- Com accedir al docstring per obtenir ajuda?
- Guardar y recuperar matrius NumPy en fitxers
- Referències:
Què és i per a què serveix NumPy ?
Python és un llenguatge fàcil d’usar, però per si sol no es pot utilitzar en aplicacions que processin dades numèriques.
En lloc d’utilitzar llistes natives de Python, la majoria d’aplicacions utilitzen els arrays que proporciona llibreria NumPy (Python Numerical) escrita a C, i que consta d’una interfície (API) que ens permet usar-les amb Python.
Per això, les matrius NumPy són més ràpides i compactes que les llistes de Python.
Una matriu consumeix menys memòria i és convenient fer servir. NumPy fa servir molta menys memòria per emmagatzemar dades i proporciona un mecanisme d’especificació dels tipus de dades que ens ajuda a prevenir errors.
Això permet el codi per optimitzar-se encara més.
Crea un projecte amb el nom de numeric, usant el gestor d’entorns virtuals ’ poetry i instal·la-hi numpy:
$ poetry new numeric --name app$ cd numeric$ poetry add numpy$ poetry shellInicia una sessió interactiva e importa numpy com a np:
$ python3import numpy as npUna llista Python pot contenir elements de diferents tipus:
> a = [1, "a", False]I un array de NumPy “també”.
Com podeu veure en aquest exemple, creem un array a partir d’una llista Python no homogènia:
> a = np.array([1, "a", False])Això és possible perquè si no especifiques el tipus de dades de l’array, la funció array utilitza el tipus de dades adequat a la llista que rep com a paràmetre.
En aquest cas, l’array és de tipus <U21>
> a.dtypedtype('<U21')Si indiquem a la funció array que ha de crear un array de tipus int, la funció ens tornarà un error tal com podeu veure a continuació:
> a = np.array([1, "a", False], dtype=int)Traceback (most recent call last): File "<stdin>", line 1, in <module>ValueError: invalid literal for int() with base 10: 'a'És interessant que ens corregeixi en aquest punt, així podem detectar més fàcilment errors per a corregir-los.
Homogeneïtat del tipus de dades en arrays de Numpy.
Quan treballem amb arrays de Numpy tots els elements de la matriu han de ser del mateix tipus si volem realitzar operacions.
Imaginem-nos dins d’un array de números accidentalment hi ha un valor que té com a format str.
Podriem mostrar l’array i ens el imprimiria bé (perquè no li hem dit explicitament el tipus de dades), però al fer qualsevol operació matemàtica no ens deixaria.
temp_pacients = np.array([ [39.6,38.4,36.5,36.4], [37.5,37.1,36.3,'x'],])print(temp_pacients)print(temp_pacients.sum()) # Dona error aquínumpy.core._exceptions._UFuncNoLoopError: ufunc 'add' did not contain a loop with signature matching types (dtype('<U32'), dtype('<U32')) -> NoneEncara que els tipus semblin iguals, Numpy té els seus propis tipus anàlegs als de Python però no idèntics (np.int, np.float32, np.complex…)
Dimensions de les matrius.
L’objecte principal de NumPy és la matriu multidimensional homogènia. És una taula d’elements (normalment números), tots del mateix tipus.
A NumPy les dimensions s’anomenen eixos (axis).
Els elements són tots del mateix tipus, conegut com l’array dtype.
Per exemple, la matriu per a les coordenades d’un punt en l’espai 3D, [1, 2, 1], té un eix. Aquest eix té 3 elements, així que diem que té una longitud de 3.
A l’exemple que es mostra a continuació, la matriu té 2 eixos. El primer eix té una longitud de 2, el segon eix té una longitud de 3.
[[1., 0., 0.], [0., 1., 2.]]Un array pot ser indexat per una tupla d’enters no negatius, per booleans, per una altra matriu, o per enters.
El ndim és el nombre de dimensions (el més habitual són 2 i 3 dimensions, però podrien ser més). El shape és una tupla de nombres enters que donen la mida de l’array al llarg de cada dimensió.
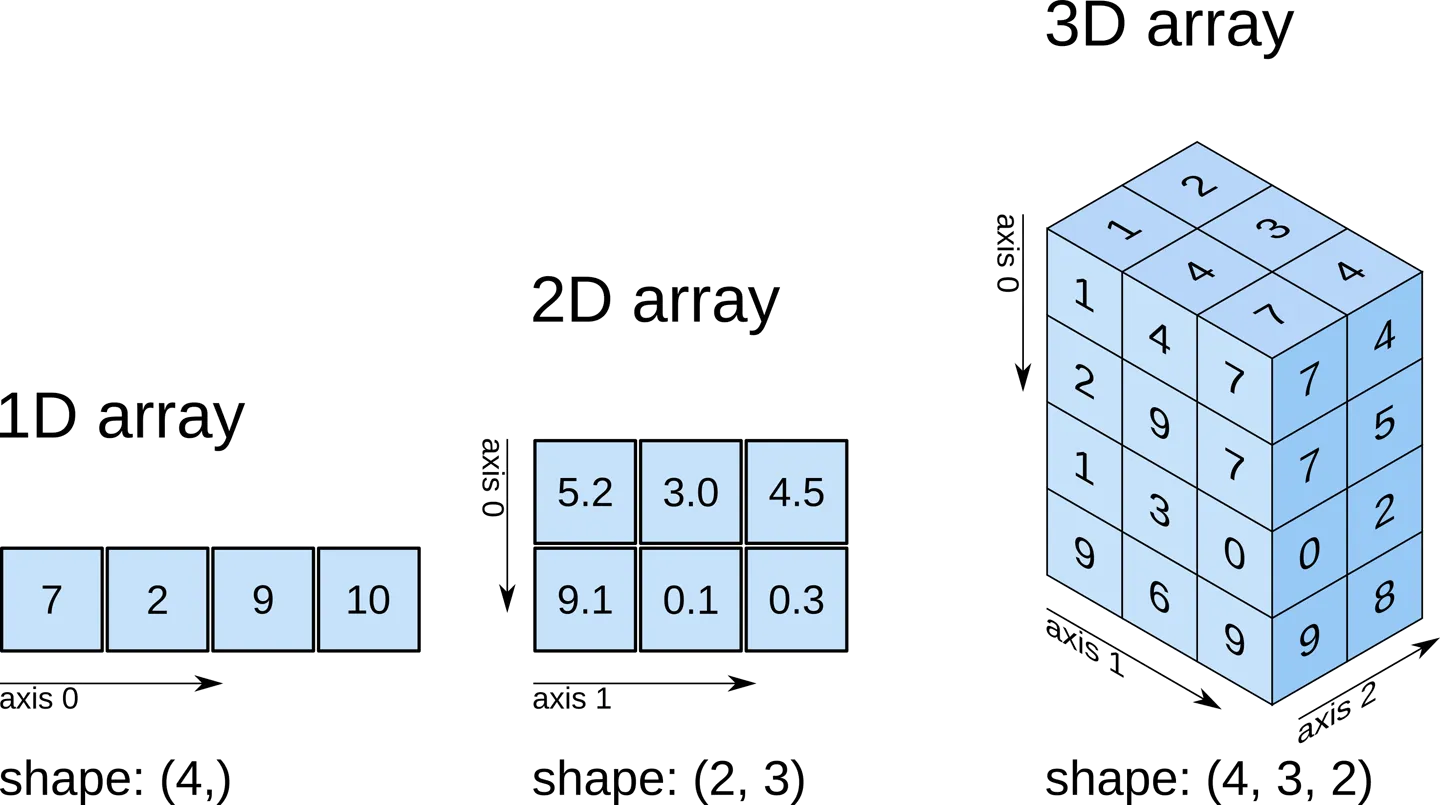
Una forma de definir les matrius de NumPy és des de llistes de Python, usant llistes enllaçades per a dades de dimensions dobles o superiors.
Per exemple:
a = np.array([1, 2, 3, 4, 5, 6])o
b = a = np.array([1, 2][3, 4][5, 6])Podem accedir als elements de la matriu usant claudàtors (square brackets).
Quan estigueu els elements d’accés, recordeu que la indexació a NumPy comença a 0.
Això significa que si voleu accedir al primer element de la vostra matriu, estareu accedint a l’element 0.
print(a[0])[1 2 3 4]Atributs i dimensions.
A NumPy, la classe que gestiona els arrays (matrius) es diu ndarray, que vol dir “N-dimensional array”.
Aquesta classe s’utilitza per a representar tant matrius (arrays de 2 dimensions) com vectors (arrays d’una dimensió). Per a matrius de 3D o més dimensions s’usa el terme tensor.
Un array es generalment un contenedor de tamany fixe d’elements del mateix tipus y tamany. El número de dimensions i elements en un array es defineix per la seva forma.
A NumPy, les dimensions es diuen eixos (axis). Això significa que si tens una matriu 2D que es veu així:
[[0., 0., 0.], [1., 1., 1.]]La matriu té 2 eixos. El primer eix té una longitud de 2 i el segon eix té una longitud de 3.
Creació d’arrays
Mètodes i atributs: np.array(), np.zeros(), np.ones(), np.empty(), np.arange(), np.linspace(), dtype
Per crear una matriu de NumPy, podeu utilitzar la funció np.array().
Tot el que necessites fer per crear una matriu simple és passar-li una llista. També pots especificar el tipus de dades de la matriu (dtype)
np.array()
import numpy as npa = np.array([1, 2, 3], dtype=np.int32)Puede visualizar aquesta matriu de totes aquestes maneres:
data[1]2data[0:2]array([1, 2])data[1:]array([2, 3])data[-2:]array([2, 3])Exemple creació i accés array temperatures.
Imaginem-nos que volem crear un array de la temperatura d’uns pacients durant uns dies.
Cada fila serà un pacient (3 pacients), cada columna serà un dia (4 dies) en el que es pren la temperatura.
L’índex de les files i de les columnes comença per 0 i acaba pel número d’elements menys 1.
import numpy as nptemp_pacients = np.array([ [39.6,38.4,36.5,36.4], [39.0,38.4,37.6,37.9], [37.5,37.1,36.3,36.0],])Per exemple, veiem que la temperatura del pacient 1 el primer dia és de 39,6; molta febre.
print(f'Temperatura pacient 1 el 1r dia.',temp_pacients[0][0])Un altre exemple, si volem obtenir la temperatura del pacient 2 (fila 1) en tots els dies.
print(f'Temperatures del pacient 2, de tots els dies.')print(temp_pacients[1])I si volem veure la temperatura del dia 1 de cada pacient, usem la notació [:], que vol dir qualsevol valor:
print(f'Temperatures del dia 1, de tots els pacients.')print(temp_pacients[:][1])Si no se li especifica cap tipus, Numpy dedueix quins elements té quan es crea la matriu.
Podem saber quin tipus és amb la funció dtype:
print(temp_pacients.dtype)Ens dona float64 en aquest cas, ens ha inferit (deduït) el tipus. És important saber amb quins tipus treballem, per evitar errors.
np.zeros() i np.ones()
A més de crear una matriu a partir d’una seqüència d’elements, podeu crear fàcilment un array plena de 0 o plena d’1s.
np.zeros(2)array([0., 0.])np.ones(2)array([1., 1.])np.empty()
També pots crear una matriu buida, La funció empty crea una matriu amb contingut aleatori i depèn de l’estat de la memòria. La raó d’utilitzar empty en comptes de zeros (o alguna cosa similar) és la velocitat - assegureu-vos domplir cada element després.
Si creem un array amb empty només s’assigna una zona de memòria principal i és molt ràpid
import numpy as np
nums = np.empty((100000,10000),dtype=int)print(nums.size)En canvi amb zeros() o ones() ha més d’assignar memòria, s’ha d’escriure tota la secció de memòria amb 0 o 1s, que és molt més lent!
import numpy as np
nums = np.ones((100000,10000),dtype=int)print(nums.size)Al crear una memòria amb empty la memòria està bruta:
import numpy as np
nums = np.empty((10,10),dtype=int)print(nums[0:4]) [ 5656527823705469221 2151596156579419888 -6326523542081462240 3157941636372412542 -1073535870585417404 -3451992775887159290Diferències entre empty i ones (o zeros):
Quina diferència hi ha entre zeros i empty? Temps de processament.
Si demanes un array amb tots zeros s’ha de gastar CPU per posar la secció de memòria assignada tota a zero.
En canvi si la demanes empty la secció de memòria estarà plena amb el que hi havia abans quan es va alliberar.
Si l’array el vas a omplir ara mateix, i l’omplés, és més eficient, però si no l’omplés del tot i que te n’oblides tindras un conjunt de dades espuries, bugs, etc.
np.arange()
Podem crear una matriu amb una sèrie d’elements (semblant al range de les llistes de Pyhton):
np.arange(4)array([0, 1, 2, 3])I fins i tot un array que conté una gamma d’intervals uniformement espaiats. Per fer-ho, especificarà el primer número, últim número i la mida del pas.
np.arange(2, 9, 2)array([2, 4, 6, 8])També podeu utilitzar np.linspace() per crear una matriu amb valors que són espaiats linealment en un interval especificat:
np.linspace(0, 10, num=5)array([ 0. , 2.5, 5. , 7.5, 10. ])Crear arrays amb slicing.
En ocasions no tindràs els valors de cap matriu ni llista, i generar-los no t’ajudarà a completar-los tots.
En aquests casos t’has de buscar la vida per omplir-la dels valors que t’interessin.
Imagina que t’han demanat una matriu 8x8 que tingui un patró 0 (blanques) / 1 (negres) com si es tratés d’un tauler d’escacs. El resultat ha de ser:
[[0 1 0 1 0 1 0 1][1 0 1 0 1 0 1 0][0 1 0 1 0 1 0 1][1 0 1 0 1 0 1 0][0 1 0 1 0 1 0 1][1 0 1 0 1 0 1 0][0 1 0 1 0 1 0 1][1 0 1 0 1 0 1 0]]Per aconseguir crear l’array, tenim dues maneres eficients i senzilles.
Utilitzar el mètode de recórrer totes les files en un bucle i posar un altre bucle per recórrer les columnes. És un enfocament senzill d’entendre i funciona.
import numpy as np
T_SIZE = 8
tauler = np.empty([T_SIZE, T_SIZE], dtype=int)
for i in range(T_SIZE): for j in range(T_SIZE): # Assigna 0 o 1 depenent de si la suma dels índexs és parell o imparell tauler[i, j] = (i + j) % 2
# print(tauler)Però podem usar un enfocament més pythonic gràcies als slices, també disponibles a Numpy i Pandas, que estan més optimitzats que els bucles que hem usat abans.
tauler = np.zeros((T_SIZE, T_SIZE), dtype=int)
tauler[1::2, 0::2] = 0 # Files senars, columnes parellstauler[0::2, 1::2] = 1 # Files parells, columnes senars
print(tauler)Fixa’t que hi ha 2 slices, un per cada fila i un per cada columna.
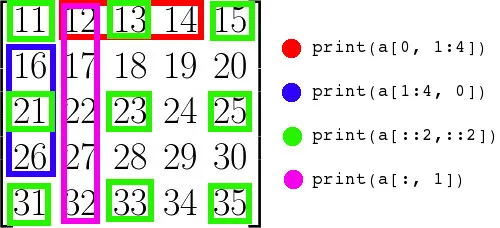
Activitat - Creació arrays
1.- Genera un array que contingui els resultats de les taules de multiplicar del 0 al 10 (la 10 inclosa) fins al 10 (des del 0 * 0 = 0 al 10 * 10 = 100) amb numpy.
{% sol %}
Solució bucles:
import numpy as np
tauler = np.zeros((11, 11), dtype=int)
for i in range(11): for j in range(11): tauler[i, j] = i * j
print(tauler)Solució range i slices, optimitzada:
import numpy as np
nombres = np.arange(11)
tauler = np.zeros((11, 11), dtype=int)
for i in range(11): tauler[i, :] = nombres * i{% endsol %}
Tipus de dades de matrius de Numpy.
El tipus de dades numèric predeterminat de Python és float64 a no ser que dedueixi algún altre (int64).
Però pots especificar quin tipus triar, i de fet és molt recomanable que ho facis per motius d’eficàcia i rendiment.
Provem-ho:
Si vols pots crear un fitxer anomenat demo_np1.py, posar aquest codi, guardar-lo i arrencar-lo (amb terminal o el teu IDE preferit)
import numpy as np
xD = np.ones([2, 3])print(xD)print(xD.dtype)print("The memory size of xD array is:",xD.itemsize*xD.size,"bytes")
x16 = np.ones([2, 3], dtype=np.int16)print(x16)print(x16.dtype)print("The memory size of x16 array is:",x16.itemsize*x16.size,"bytes")print("Size of one element from x16 is ",x16.itemsize, "bytes")Els resultats que obtenim són:
[[1. 1. 1.] [1. 1. 1.]]float64The memory size of xD array is: 48 bytes[[1 1 1] [1 1 1]]int16The memory size of x16 array is: 12 bytesSize of one element from x16 is 2 bytesAmb aquesta comprovació hem descobert 2 atributs de la matriu, que multiplicats ens donen el tamany en bytes de l’array Numpy:
- x16.itemsize Tamany de cada element.
- x16.size Número d’elements
Les variables de Python no té cap importància que ocupin 64 bits (és el tamany de paraula del processador), quan programis olvida’t de tot això.
Només quan has de gestionar arrays de dades de gran volum es quan has de tenir en compte l’espai que ocuparan i minimitzarles.
En les memòries caché del processador és fonamental aprofitar al màxim l’espai! Estem fent big data, i quan gestionem grans volums de dades cal tenir en compte això, que és molt important.
Saber el tamany i forma d’un array.
Mètodes: ndarray.ndim, ndarray.size, ndarray.shape
ndarray.ndim
Número de dimensions de la matriu.
ndarray.size
Número total de elements de la matriz. És igual al producte dels elementos de la forma.
ndarray.shape
Tupla d’enters que indiquen el número d’elements que hi ha a cada dimensió de la matriu.
Per exemple, si tens un Conjunt de 2-D amb 2 files i 3 columnes, la forma és (2, 3).
Provarem els 3 atributs amb aquest array:
array_example = np.array([[[0, 1, 2, 3], [4, 5, 6, 7]], [[0, 1, 2, 3], [4, 5, 6, 7]], [[0 ,1 ,2, 3], [4, 5, 6, 7]]])
print(array_example.ndim)3
print(array_example.size)24
print(array_example.shape)(3, 2, 4)Es pot remodelar una matriu ?
I tant, usant arr.reshape() podràs definir una nova forma a la matriu sense canviar les dades.
La única condició és que la nova matriu ha de tenir el mateix tamany que la original.
Per exemple, pots remodelar una matriu de (6, 2) a (3, 4) perquè el tamany (size) en ambdues és el mateix, 12.
Aquí tenim un exemple per transformar una matriu (6, 1) a (3, 2):
a = np.arange(6)
print(a)[0 1 2 3 4 5]
b = a.reshape(3, 2)
print(b)[[0 1] [2 3] [4 5]]Activitat - Preguntes i exercici.
Pr1- Quina és la sintaxi corrrecta per mostrar el número 8 ??
arr = np.array([[1,2,3,4,5], [6,7,8,9,10]])- print(arr[7,2])
- print(arr[0,2])
- print(arr[1,2])
- print(arr[2,3])
Pr2- Quina és la sintaxi corrrecta per mostrar els números [3, 4, 5] ??
arr = np.array([1,2,3,4,5,6,7])- print(arr[2,5])
- print(arr[3,6])
- print(arr[2,4])
- print(arr[2,6])
Pr3- Què mostrarà per pantalla el següent codi ?
A = np.array([ ['a', 'b', 'c'], ['d', 'e', 'f'], ['g', 'h', 'i']])
print(A[:, :2])1.[['a' 'b' 'c'] ['d' 'e' 'f'] ['g' 'h' 'i']]
2.[['b' 'c'] ['e' 'f'] ['h' 'i']]
3.[['a' 'b'] ['d' 'e'] ['g' 'h']]
4.[['a'] ['d'] ['g']]Pr4- Quina és la forma correcta d’obtenir el tipus de dades a Numpy de l’array arr ?
- arr.types
- arr.shape
- arr.type
- arr.dtype
- arr.ndim
Pr5- Quina relació hi ha entre la mida dels objectes (com ara llistes i tipus de dades) a la memòria de la biblioteca estàndard de Python i la biblioteca NumPy? Sabent això, quines són les implicacions per al rendiment?
-
Els objectes Python estàndard ocupen molta més memòria per emmagatzemar que els objectes NumPy; Les operacions sobre objectes estàndard comparables de Python i NumPy es completen aproximadament al mateix temps.
-
Els objectes NumPy ocupen molta més memòria que els objectes Python estàndard; Les operacions sobre objectes NumPy es completen molt ràpidament en comparació amb objectes comparables en Python estàndard.
-
Els objectes NumPy ocupen molta menys memòria que els objectes Standard Python; Les operacions sobre objectes Python estàndard es completen molt ràpidament en comparació amb objectes comparables a NumPy Object.
-
Els objectes Python estàndard ocupen més memòria que els objectes NumPy; Les operacions sobre objectes NumPy es completen molt ràpidament en comparació amb objectes comparables en Python estàndard.
Ex1. Ens han donat aquestes llistes que representen els resultats de proves de glucosa en sang (mg/dL) de 4 pacients en 3 moments diferents del dia (matí, tarda, nit).
[95, 105, 99], # Pacient 1[89, 112, 102], # Pacient 2[110, 129, 115],# Pacient 3[100, 108, 104] # Pacient 4Fes un programa que realitzi el següent:
- Guarda tots els resultats en un array de numpy del tipus més adient i que ocupi el mínim espai possible.
- Mostra el contingut, la forma de l’array i el tamany de memòria que ocupa.
- Mostra les dades de l’últim pacient.
- Mostra les dades de tots els paients pel matí.
Ex2. Transforma aquest array d’1x12 (temperatures de cada mes) a 2 arrays de 2 files i 3 columnes. Un array de 3 dimensions.
temperatures = np.array([29.3, 42.1, 18.8, 16.1, 38.0, 12.5, 12.6, 49.9, 38.6, 31.3, 9.2, 22.2]){% sol %}
Pr1 - 3, Pr2 - 1, Pr3 - 3, Pr4 - 2, Pr5 - 4.
Ex1.
import numpy as np# Dades dels resultats de glucosa en sang dels pacientsresultats = [ [95, 105, 99], # Pacient 1 [89, 112, 102], # Pacient 2 [110, 120, 115], # Pacient 3 [100, 108, 104] # Pacient 4]resultats_array = np.array(resultats, dtype="int16")
print("Contingut de l'array:", resultats_array)print("Forma de l'array:", resultats_array.shape)print("Tamany de memòria que ocupa:", resultats_array.nbytes, "bytes")
print("\nDades de l'últim pacient:")print(resultats_array[-1])print("\nDades de tots els pacients pel matí:")print(resultats_array[:, 0])Ex2.
temperatures = np.array([29.3, 42.1, 18.8, 16.1, 38.0, 12.5, 12.6, 49.9, 38.6, 31.3, 9.2, 22.2])
temperatures.reshape(3, 4)
print(temperatures)print(temperatures.shape)Resultat esperat:
array([[29.3, 42.1, 18.8], [16.1, 38. , 12.5]],
[[12.6, 49.9, 38.6], [31.3, 9.2, 22.2]]])(2, 2, 3){% endsol %}
Operacions amb valors de matrius.
Ordenació
Provem els mètodes np.sort() i np.concatenate()
Ordenar un element és simple amb np.sort()
Ho provarem amb aquesta matriu de números desordenats:
arr = np.array([2, 1, 5, 3, 7, 4, 6, 8])np.sort(arr)array([1, 2, 3, 4, 5, 6, 7, 8])També funciona amb matrius amb text.
Concaternació
Si inicies aquestes matrius, puedes concatenar-les con np.concatenate().
a = np.array([1, 2, 3, 4])
b = np.array([5, 6, 7, 8])
np.concatenate((a, b))
array([1, 2, 3, 4, 5, 6, 7, 8])Un altre exemple:
x = np.array([[1, 2], [3, 4]])
y = np.array([[5, 6]])
np.concatenate((x, y), axis=0)array([[1, 2], [3, 4], [5, 6]])Transposar matrius.
Ho pots fer amb l’atribut T o el mètode .transpose()i serveix per intercanviar els continguts dels eixos.
Provem de transposar aquesta matriu:
arr = np.arange(6).reshape((2, 3))
arrarray([[0, 1, 2], [3, 4, 5]])arr.transpose()array([[0, 3], [1, 4], [2, 5]])También puedes usar arr.T:
arr.Tarray([[0, 3], [1, 4], [2, 5]])Invertir ordre: flip
La funció np.flip() et permet donar la volta a la matriu. Anem a veure exemples.
Invertir contingut matriu 1D
arr = np.array([1, 2, 3, 4, 5, 6, 7, 8])reversed_arr = np.flip(arr)print('Reversed Array: ', reversed_arr)Reversed Array: [8 7 6 5 4 3 2 1]Invertir contingut matriu 2D
arr_2d = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])reversed_arr = np.flip(arr_2d)print(reversed_arr)[[12 11 10 9] [ 8 7 6 5] [ 4 3 2 1]]Invertir files d’una matriu 2D
reversed_arr_rows = np.flip(arr_2d, axis=0)
print(reversed_arr_rows)[[ 9 10 11 12] [ 5 6 7 8] [ 1 2 3 4]]Invertir columnes d’una matriu 2D
reversed_arr_columns = np.flip(arr_2d, axis=1)
print(reversed_arr_columns)[[ 4 3 2 1] [ 8 7 6 5] [12 11 10 9]]Invertir només una fila d’una matriu 2D
arr_2d[1] = np.flip(arr_2d[1])print(arr_2d)[[ 1 2 3 4] [ 8 7 6 5] [ 9 10 11 12]]Invertir només una columna d’una matriu 2D
arr_2d[:,1] = np.flip(arr_2d[:,1])
print(arr_2d)[[ 1 10 3 4] [ 8 7 6 5] [ 9 2 11 12]]Còpies de matrius: view vs copy.
Per a fer còpies netes de matrius Numpy proporciona 2 mètodes: view i copy
El view (o l’operador =) serveix per crear un nou objecte d’array que agafa les mateixes dades que l’array original (còpia superficial).
Les vistes són un concepte important de NumPy. Ens permeten salvar memòria i són més ràpides.
Aquest concepte és anàleg a les vistes que proporcionen diverses bases de dades basades SQL.
El que és important saber és que modificar les dades d’una vista també modifica la matriu original.
Creem una matriu a i creem una còpia d’alguns valors en una matriu vista b1. Veurem com els valors d’a canvien quen s’edita un valor de b1 (i viceversa).
a = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
b1 = a[0, :]
b1array([1, 2, 3, 4])b1[0] = 99
b1array([99, 2, 3, 4])aarray([[99, 2, 3, 4], [ 5, 6, 7, 8], [ 9, 10, 11, 12]])En canvi, si uses el mètode copy farà una còpia completa de l’array y les dades. Així, si edites un valor de la còpia no canvia a la matriu original (ni al revés).
Pots fer una còpia amb aquesta instrucció i provar-ho:
b2 = a.copy()b2[0] = 50print(b2)```pyarray([50, 2, 3, 4])
```pyprint(a)array([[99, 2, 3, 4], [ 5, 6, 7, 8], [ 9, 10, 11, 12]])
Aplanament de conjunts multidimensionals
Hi ha dues maneres populars d’aplanar un array (convertir-lo a un array 1D):
flatten() i .ravel().
Ens interessa, quan volem guardar tota la matriu en una llista; ja que hi ha llibreries que només accepten llistes i no arrays.
La diferència principal entre tots dos és que la nova matriu creada usant ravel() és en realitat una referència a la matriu origen (és a dir, una vista). Això significa que qualsevol canvi a la nova matriu també afectarà la matriu original.
En canvi, quan uses flatten fas una còpia dura exacta i llavors els canvis a la nova matriu no afecten a la matriu original.
Provem de fer la còpia amb el mètode flatten:
x = np.array([[1 , 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])x.flatten()array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])a1 = x.flatten()a1[0] = 99
print(x) # Original array[[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]]
print(a1) # New array[99 2 3 4 5 6 7 8 9 10 11 12]Provem de fer la vista amb el mètode ravel:
a2 = x.ravel()
a2[0] = 98
print(x) # Original array[[98 2 3 4] [ 5 6 7 8] [ 9 10 11 12]]
print(a2) # New array[98 2 3 4 5 6 7 8 9 10 11 12]Valors constants de numpy.
Numpy conté constants que són interessants en el món de la ciència; com np.pi (el famós número PI=3,14159…), logaritmes i el valor Inf, per a especificar un número infinit.
>>> print(round(np.pi,6))3.141593>>> np.array([1]) / 0array([ Inf])Tractament valors no existents: NaN.
Un dels problemes de tractar amb dades massives és que és freqüent trobar-te una sèrie en que hi ha algún buit perquè la dada no s’ha pogut registrar o és desconeix.
En llenguatges de programació (pex Java) o de bases de dades (SQL) existeix el valor nul. Per exemple, una persona pot tenir l’atribut telefon amb valor null. Però aquest nul que vol dir? Que no té telèfon o que no sabem si te telèfon perquè no li hem preguntat o no l’ha registrat?
En el cas de seqüències de dades és evident que no és el mateix cas, hi ha un buit i aquest buit sempre estarà, però s’ha d’omplir amb alguna cosa, i està clar que no és un número (no ens podem inventar les dades numèriques).
D’aquí ve el nom NaN, Not a Number (no és un número). Que és? Ves a saber 🤔
Pots pensar que els de Python, concretament els de NumPy som una mica frescos, però es una solució molt pensada i raonada.
En un llenguatge com Java o C en un array de números només pot haver-hi números; per tant, si falten dades en una seqüència has de reflectir aquest fet posant 0 o -1 o ves a saber què, el que suposa a la llarga problemes i bugs.
Et poden dir que Python no es un gran llenguatge perquè no té tipus forts com Java, però amb arrays de dades numèriques és tot el contrari 🙂.
Per eficiencia a Python i Numpy s’utilitza NaN quan vol dir “Not a Number”. Amb numpy representem el valor NaN amb la constant np.nan
Si sumo un número amb un nan que passa?
>>> import numpy as np>>> np.nan + 3nanEfectivament, el valor segueix sent indefinit; nan.
Tal com s’explica en aquest article sobre els valors NaN a Numpy i Pandas, qualsevol operació sobre tot un array que té almenys un NaN té com a resultat un NaN perquè no sabem de quina manera afectarà a la operació suma o qualsevol altre? Està completament indefinit!
És important definir alguna estratègia de què fer amb aquests registres amb valor np.nan, depèn d’importància de les dades.
No obstant, com que l’opció més habitual a l’hora de tractar matrius és ignorar el que molesta perquè et fa pensar i qüestionar coses, l’objecte array permet fer algunes operacions ignorant els NaN: Per exemple array.nansum, etc
Ampliarem aquestes reflexions sobre què fer amb columnes que tinguin algun valor NaN quan veiem la llibreria Pandas.
El concepte de NaN existia fins i tot abans de la creació de Python. L’estàndard IEEE per a l’aritmètica de coma flotant (IEEE 754) va introduir NaN el 1985.
NaN és un valor especial de coma flotant que no es pot convertir a cap altre tipus que no sigui flotant.
Per observar les propietats de NaN, creem una matriu Numpy amb valors de NaN.
import numpy as nparr = np.array([1, np.nan, 3, 4, 5, 6, np.nan])pritn(arr)Sortida: [ 1. nan 3. 4. 5. 6. nan]
Operacions matemàtiques sobre una matriu Numpy amb NaN
Intentem cridar algunes funcions bàsiques a la matriu Numpy.
cprint(arr.sum())print(arr.max())Sortida: nan nan
Una opció bastant freqüent és que en la sèrie concreta de dades que vas a analitzar puguis ignorar les dades ausents. Per aquest motiu, Numpy ofereix mètodes que ignoren els valors de NaN mentre es realitzen operacions matemàtiques.
Numpy us ofereix mètodes com np.nansum() i np.nanmax() per calcular la suma i el màxim després d’ignorar els valors de NaN a la matriu.
$ np.nansum(arr)19.0$ np.nanmax(arr)6.0Si tens activat l’autocompleció al vostre IDE, podràs veure la llista d’opcions mentre treballeu amb np.nan.
nanmean, nanmin …
Comprovació dels valors de NaN
Per comprovar els valors de NaN en una matriu Numpy, podeu utilitzar el mètode np.isnan(). Això genera una màscara booleana de la mida de la matriu original.
La matriu de sortida té True per als índexs que són NaN a la matriu original i False per a la resta.
Per exemple, en la nostra matriu; si apliquem la instrucció print(np.isnan(arr))
[1, np.nan, 3, 4, 5, 6, np.nan, 8]
La sortida serà:
[False True False False False False True]Per saber quants Nan tenim en una matriu:
arr = np.array([1, np.nan, 3, 4, 5, 6, np.nan, 8])print(np.isnan(arr))print("Nan values in arr = ", np.count_nonzero(np.isnan(arr)))Resultat:
[False True False False False False True]Nan values in arr = 2Són dos NaN iguals entre si?
Aquesta pot ser una pregunta confusa. Intentem respondre-ho executant algun codi Python.
a = np.nanb = np.nanAquestes dues declaracions inicialitzen dues variables, a i b amb nan. Intentem equiparar els dos.
$ a == bFalseA Python també tenim l’ operador is . Intentem utilitzar-ho per comparar les dues variables.
$ a is bTrueLa raó d’això és que l’operador == compara els valors dels operands i comprova la igualtat de valors. L’operador is, en canvi, comprova si els dos operands fan referència o no al mateix objecte. De fet, pots imprimir els ID de a i b i veure que es refereixen al mateix objecte.
$ id(a)139836725842784
$ id(b)139836725842784Filtratge, edició i esborrat d’elements d’arrays.
Abans d’explicar com s’elimina contingut als arrays, hem de recordar com funcionen per dins.
Internament, els arrays de Numpy funcionen amb C (llenguatge multiplataforma inclòs en tots el SO) i el que fa aquest és agafar un tros de memòria RAM on es pugui guardar tot l’array de forma consecutiva.
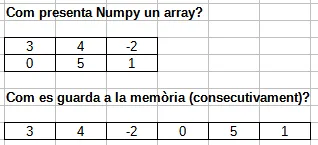
Per tant, si la edició de l’array consisteix en intercanviar un valor per un altre, es podrà fer automàticament perquè al final l’array seguirà ocupant el mateix.
En canvi, tots els canvis que impliquin afegir o treure espai en la memòria reservada (eliminar files, columnes…) crearan automàticament una còpia modificada de l’array, per no perdre informació accidentalment.
Esborrat files o columnes.
Provarem tot això amb el mètode per eliminar files o columnes concretes, np.delete. Ens permet eliminar la segona fila (primera = 0, segona = 1, …). Si posem axis=0 eliminarà files, axis=1 columnes.
arr = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])np.delete(arr, 1, axis=0)print(arr)Resultat.
[[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]]Com és que no s’ha eliminat la fila que li hem dit ? No ha passat res! Perquè Numpy no pot retornar l’array modificat, sinó una còpia modificada.
Si ens interessa mantenir l’array original, podem fer-ho amb la instrucció:
arr_cpy = np.delete(arr, 1, axis=0)print(arr_cp)
[[ 1 2 3 4] [ 9 10 11 12]]En canvi, si només volem tenir el nou array, podem sobreescriure l’array original i així estalviar memòria:
arr = np.delete(arr, 1, axis=0)print(arr)Selecció valors nou array per index, slices.
Podeu indexar i llescar (retallar) els arrays NumPy de la mateixa manera que podeu tallar llistes de Python.
data = np.array([1, 2, 3])
data[1]2
data[0:2]array([1, 2])
data[1:]array([2, 3])
data[-2:]array([2, 3])Selecció valors nou array per condicions.
Si voleu seleccionar valors de la vostra matriu que compleixin certes condicions, és molt senzill amb NumPy.
Per exemple, pots crear una nova matriu només amb els valors menors de 5.
a = np.array([[1 , 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])print(a[a < 5])[1 2 3 4]També podeu seleccionar, per exemple, números que siguin iguals o superiors a 5, i utilitzar aquesta condició per indexar una matriu.
five_up = (a >= 5)print(a[five_up])[ 5 6 7 8 9 10 11 12]Seleccionar elements divisibles per 2:
divisible_by_2 = a[a%2==0]
print(divisible_by_2)[ 2 4 6 8 10 12]O pots seleccionar elements que compleixin diverses condicions usant operadors :
c = a[(a > 2) & (a < 11)]print(c)[ 3 4 5 6 7 8 9 10]També és important saber quins elements d’un array compleixen les condicions o no; per filtrar números o altres valors categòrics.
five_up = (a > 5) | (a == 5)
print(five_up)[[False False False False] [ True True True True] [ True True True True]]Si l’element que busques no existeix a l’array, llavors el retornat La varietat d’índexs estarà buida. Per exemple:
not_there = np.nonzero(a == 42)print(not_there)(array([], dtype=int64), array([], dtype=int64))Operacions numèriques amb matrius
Secció: suma, resta, multiplicació, divisió, potència.
Primer, provarem les operacions amb dos arrays, un es diu “data”. y un altre que es diu “ones” Podem fer la suma únicament amb l’operador +.
data = np.array([1, 2])ones = np.ones(2, dtype=int)print(data + ones)[2 3]Pots fer més operacions (restar, multiplica,r dividir)
data - onesarray([0, 1])
data * dataarray([1, 4])
data / dataarray([1., 1.])sum()
Si vols calcular la suma dels elements en una array, va molt bé el mètode sum(). Funciona per arrays de qualsevol dimensió.
a = np.array([1, 2, 3, 4])a.sum()10Per fer sumes d’arrays bidimensionals pots especificar l’eix on començar:
b = np.array([[1, 1], [2, 2]])Suma per eix de les files:
b.sum(axis=0)array([3, 3])Suma per eix de les columnes:
b.sum(axis=1)array([2, 4])En moltes ocasions, ens pot interessar fer operació entre un array i un sol nombre (també anomenat operació entre un vector i un escalar) o entre conjunts de dues mides diferents.
Per exemple, tenim una matriu amb informació sobre la distància en quilòmetres de ciutats i voleu convertir-la a milles (terrestres).
Podeu realitzar aquesta operació amb:
data = np.array([1.0, 2.0])data * 1.6array([1.6, 3.2])Per provar les potències, practicarem en les que més coneixem els informàtics:
2n
Per exemple, ja sabeu que amb 8 bits es poden representar 256 valors:
28 = 256
Per exemple, podem tenir una variable que tingui valors entre -128 i 127. I també que 8 bits són 1 Byte.
També sabeu que:
216 = 65536 bits
Llavors, creeu una matriu de de 8 x 2; que tingui el següent aspecte:
[[ 2 4 8 16 32 64 128 256] [ 512 1024 2048 4096 8192 16384 32768 65536]]quadlist = [2**i for i in range(1, 17)]quadarr = np.array(quadlist).reshape(2,8)print(quadarr)Exemples problemes de matrius.
Una firma d’automòbils disposa de dues plantes de fabricació una a Espanya i una altra a Anglaterra, on fabrica dos models de cotxes M1 i M2, de tres colors x, i, z.
La seva capacitat de producció diària a cada planta està donada per les matrius següents (A per a Espanya i B per a Anglaterra).
Matriu A
[[ 300, 95], [ 250, 100], [ 200, 100]]Matriu B
[[ 190, 90], [ 200, 100], [ 150, 80]]Crea les matrius i respon:
a. Determinar la representació matricial de la producció total per dia.
b. Si s’eleva la producció a Espanya un 20% i es disminueix a Anglaterra un 10% quina matriu representa la nova producció total?
Solució (codi i resultat):
ar_vendes_es = np.array([ [ 300, 95], [ 250, 100], [ 200, 100]])ar_vendes_uk = np.array([ [ 190, 90], [ 200, 100], [ 150, 80]])
print('a) Determinar la representación matricial de la producción total por día.')ar_vendes_total_1 = ar_vendes_es + ar_vendes_ukprint(ar_vendes_total_1)
print('b) Si se eleva la producción en España un 20% y se disminuye en Inglaterra un 10% ¿qué matriz representa la nueva producción total?')ar_vendes_es_2 = ar_vendes_es*1.2ar_vendes_uk_2 = ar_vendes_uk*0.9
ar_vendes_total_2 = ar_vendes_es2 + ar_vendes_uk_2print(ar_vendes_total_2)Resultat A.[[490 185] [450 200] [350 180]]
Resultat B[[300 95] [250 100] [200 100]]Si les dimensions en un problema no són compatibles, apareixerà un ValueError.
Generar números aleatoris
La generació de nombres aleatoris (en realitat, números pseudoaleatòries repetibles) és una part important molts algorismes numèrics i d’aprenentatge automàtic.
Per exemple, pots generar una matriu de 2 x 4 d’enters aleatoris entre 0 i 4 amb el mètode np.random.default_rng:
rng = np.random.default_rng()a = rng.integers(5, size=(2, 4)) # may varyprint(a)També pots establir endpoint=True per a incloure el número més alt (5 en el nostre cas).
En versions anteriors de Numpy els números aleatoris es creaven d’aquesta manera:
matrix_1 = np.random.randint(10, size=(6,4))I encara es pot fer de les dues maneres per motius de retrocompatibilitat, però a la documentació ens animen a usar Generator.integers i els nous mètodes.
Operacions estadístiques amb matrius
Funcions disponibles: màxim, mínim, suma, mitjana, etc…
NumPy també realitza funcions d’agregació, que són funcions que s’apliquen sobre més d’un element de l’array (una o més files, una o més columnes, o l’array sencer) Les funcions d’agregació més habituals són: min, max, i sum.
També pots calcular fàcilment la mitjana aritmètica mean, std (desviació estàndard), i més.
Creem aquest array per a provar-los:
a = np.array([[0.45053314, 0.17296777, 0.34376245, 0.5510652], [0.54627315, 0.05093587, 0.40067661, 0.55645993], [0.12697628, 0.82485143, 0.26590556, 0.56917101]])És molt comú voler sumar tots els elements d’una fila o columna.
Per defecte, cada La funció d’ agregació NumPy retornarà l’agregat (suma) de tota la matriu.
A trobar la suma o el mínim dels elements de la seva matriu, executa:
a.sum()4.8595784O:
a.min()0.05093587Pots especificar en quin eix s’aplica la funció d’agregació. Per exemple, pot trobar el valor mínim dins de cada columna especificant axis = 0.
a.min(axis=0)array([0.12697628, 0.05093587, 0.26590556, 0.5510652 ])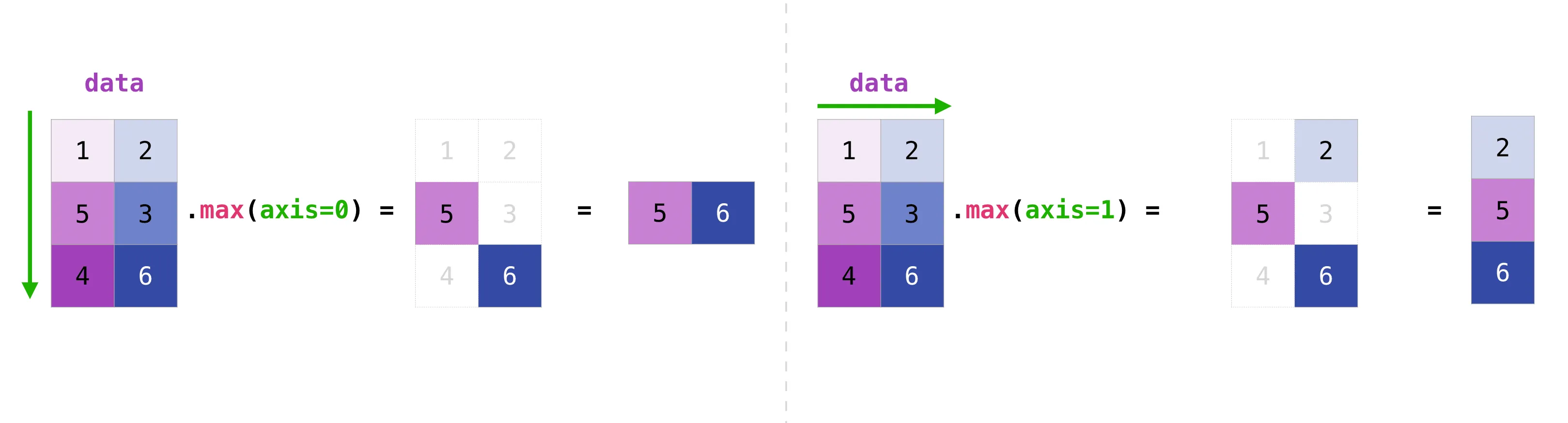
Els quatre valors esmentats anteriorment corresponen al nombre de columnes de la matriu. Amb una matriu de quatre columnes, obtindre, quatre valors com a resultat.
Pot agregar tots els valors en una matriu i pot agregar-los a través columnes o files amb el paràmetre axis. Per il·lustrar aquest punt, mira un conjunt de dades lleugerament modificat:
data = np.array([[1, 2], [5, 3], [4, 6]])
dataarray([[1, 2], [5, 3], [4, 6]])
data.max(axis=0)array([5, 6])
data.max(axis=1)array([2, 5, 6])Un cop hagi creat les seves matrius, pot afegir-les i multiplicar-les usant operadors aritmètics si tens dues matrius que són de la mateixa mida.
data = np.array([[1, 2], [3, 4]])
ones = np.array([[1, 1], [1, 1]])
data + onesarray([[2, 3], [4, 5]])Així pots visualitzar el màxim, mínim i sumatori dels valors d’un array sencer:
data.max()6data.min()1data.sum()21També podem generar la mitjana i la desviació típica o estàndard d’un vector amb 300 números aleatoris:
import numpy as npvector = np.random.randint(100, size=300)print("Average: %.2f" % float(np.average(vector)))print("Deviation: %.2f" % float(np.std(vector)))
Average: 47.88Deviation: 29.78Com aconseguir valors únics.
Pots trobar els elements únics en una matriu fàcilment amb np.unique. Veiem un exemple:
a = np.array([11, 11, 12, 13, 14, 15, 16, 17, 12, 13, 11, 14, 18, 19, 20])unique_values = np.unique(a)print(unique_values)[11 12 13 14 15 16 17 18 19 20]Si en compte dels valors ens interessen els index, tenim el paràmetre return_index=True
unique_values, indices_list = np.unique(a, return_index=True)print(indices_list)[ 0 2 3 4 5 6 7 12 13 14]Per obtenir el recompte de freqüències el més útil és usar l’argument return_counts dins d’np.unique()
unique_values, occurrence_count = np.unique(a, return_counts=True)print(occurrence_count)[3 2 2 2 1 1 1 1 1 1]Veiem un exemple amb matrius 2D:
a_2d = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12], [1, 2, 3, 4]])unique_values = np.unique(a_2d)print(unique_values)[ 1 2 3 4 5 6 7 8 9 10 11 12]Si no has especificat l’eix (paràmetre axis), la matriu 2D s’aplanarà (es transformarà a 1D).
Per trobar les files úniques, especifica axis = 0 i per a les columnes axis = 1.
unique_rows = np.unique(a_2d, axis=0)
print(unique_rows)[[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]]Una de les dades que més ens interessa en estadística és la moda, que és saber quin (o quins) valors es repeteixen més i quantes vegades dins d’una mostra (dins de l’array).
Calculem la única moda d’un array.
# create NumPy array of values with only one modex = np.array([2, 2, 2, 3, 4, 4, 5, 5, 5, 5, 7])
#find unique values in array along with their countsvals, counts = np.unique(x, return_counts=True)# print("Valors ",vals)# print("Núm.Vegades ",counts)
# Numero vegades que es repeteix la moda.num_oc = counts.max()
# Posició on es troba la moda.id_moda = list(counts).index(num_oc)
# Valor de la moda, per fivalor_moda = vals[id_moda]print('Valor moda ',valor_moda)print('Núm. repeticions ',num_oc)Com podeu veure, no és tant senzill com els altres càlculs; però el mètode unique ens ha facilitat les coses.
Si simplement ens demanen representar de forma còmode les ocurrències de cada valor, les podem aconseguir creant un nou array a partir de la operació unique:
np.array(np.unique(x, return_counts=True)).T array([[ 1, 5], [ 2, 3], [ 5, 1], [25, 1]])I què passa si tenim més d’una moda ??
Tenim diverses opcions, com un algorisme més llarg, o bé usar una altra llibreria bastant habitual scipy que ens ajudi amb un mètode mode. En aquests articles es plantegen les dues solucions.
Preguntes i exercicis d’operacions i estadístiques amb matrius.
Pr6. Explica amb les teves paraules la principal diferència entre els mètodes view i copy.
Pr7. Què fa aquest codi ? Només una opció és correcta.
import numpy as npa = np.array([[9, 3], [5, 10], [7, 6]])print(a.mean(axis=0))- Calcula la mitjana aritmètica de tots els números de la matriu, i retorna un únic resultat.
- Calcula la mitjana aritmètica de les files de la matriu, i retorna 2 resultats.
- Calcula la mitjana aritmètica de les columnes de la matriu, i retorna 3 resultats.
- Cap de les respostes és correcta.
Ex4. Generar i tractar arrays aleatoris:
Genera un array amb 10 elements amb edats de diversos alumnes de cicles (mínim 16 anys).
Genera un segon array també de 10 elements amb alguns dels 8 grups i rh sanguinis (“A+”,“A-”…). Pista: usa la funció choose.
Posteriorment, afegeix manualment a les matrius 3 alumnes majors de 30 (3 edats i 3 grups sanguinis).
Ex5. Operacions i estadístiques Tenim les qualificacions dels examens de 3 alumnes en 2 mòduls (assignatures) del trimestre 1. I un altre array de les mateixes dimensions del trimestre 2 i final (decimals)
import numpy as np# Qualificacions dels alumnes en dos trimestrestrimestre1 = np.array([ [7.5, 8.0], [6.0, 7.5], [8.5, 9.0]])trimestre2 = np.array([ [8.0, 5.5], [4.0, 8.0], [9.0, 9.5]])Realitza les següents:
- Suma valors dels 2 arrays i guarda la suma en un nou array.
- Multiplica per 1.1 els valors de la última filera.
- Divideix per 2 els valors de l’array.
- Calcula la mitjana aritmètica de notes del mòdul que està a la primera posició.
{% sol %}
Pr7. Resposta: 2.
Ex4.
import numpy as np
grups_sanguinis = ["A+", "A-", "B+", "B-", "AB+", "AB-", "O+", "O-"]
# Generar un array aleatori amb edats entre 16 i 30num_alumnes = 10edats = np.random.randint(16, 31, num_alumnes)
# Generar un array aleatori amb grups sanguinisgrups = np.random.choice(grups_sanguinis, num_alumnes)
# Afegir manualment 3 alumnes majors de 30edats_extens = np.append(edats, [35, 40, 45])grups_extens = np.append(grups, ["A+", "B-", "O+"])
print("Array d'edats:")print(edats_extens)print("\nArray de grups sanguinis:")print(grups_extens)Ex5
# Sumar valors dels dos arrays i guardar la suma en un nou arraysuma_trimestres = trimestre1 + trimestre2
print("Suma dels dos trimestres:")print(suma_trimestres)
# Multiplicar per 1.1 els valors de la última filerasuma_trimestres[-1] *= 1.1
print("\nSuma amb última filera multiplicada per 1.1:")print(suma_trimestres)
# Dividir per 2 els valors de l'arraydivisio_trimestres = suma_trimestres / 2
print("\nArray dividit per 2:")print(divisio_trimestres)
# Calcular la mitjana aritmètica de les notes del mòdul,# que està a la primera posició (columna 0)mitjana_modul1 = np.mean(divisio_trimestres[:, 0])
print("\nMitjana aritmètica de les notes del mòdul 1:")print(mitjana_modul1){% endsol %}
Exemple pràctic ús arrays. Quadres de Punnet.
En el context dels gats i el pelatge, assumim que l’al·lel per al pelatge negre és dominant (P) i l’al·lel per al pelatge blanc és recessiu (p).
Després, tenim que l’al·lel de la cua llarga és C i dominant i el de cua curta la c.
Els gamets possibles del creuament d’un gat i una gata heterozigots pel gen del pelatge i pel de la cua són:
- Gat (PpCc): PC, Pc, pC, pc
- Gata (PpCc): PC, Pc, pC, pc
Dibuixa el quadre de Punnet 4 x 4 resultant.
Quan el tinguis, respon i demostra amb Python les probabilitats que el descendent tingui cua curta i pèl llarg.
import numpy as np
allels = ['PC', 'Pc', 'cP', 'pc']
punnett_square = np.empty((len(allels), len(allels)), dtype='U4')
# Llenar el cuadro de Punnett con las combinaciones de alelosfor i in range(len(allels)): for j in range(len(allels)): punnett_square[i, j] = allels[i][0] + allels[j][0] + allels[i][1] + allels[j][1]
print(punnett_square)
# Vols saber les probabilitats de llarga i pel curt.elements = ['Ppcc', 'PPcc', 'pPcc']
# Aplano la matriu per fer el càlcul més senzill.flat_punnett = punnett_square.flatten()# Comptar quantes vegades apareix cada element a la matriucounts = [np.sum(punnett_square == element) for element in elements]
print(f"Probabilitats = {np.sum(counts)/len(flat_punnett)}\n")Com accedir al docstring per obtenir ajuda?
La biblioteca Numpy, com qualsevol bona feina creada en Python, inclou documentació d’ajuda en format docstring. En la majoria de casos, aquest docstring conté un resum de l’objecte i com utilitzar-lo. Python té la funció help() incorporada per a accedir a aquesta informació. Per exemple:
help(max)Help on built-in function max in module builtins:
max(...) max(iterable, *[, default=obj, key=func]) -> value max(arg1, arg2, *args, *[, key=func]) -> value
With a single iterable argument, return its biggest item. The default keyword-only argument specifies an object to return if the provided iterable is empty. With two or more arguments, return the largest argument.
...Aquesta notació també t’anirà bé per obtenir els mètodes que pots aplicar dins de l’objecte que has creat i altres objectes que conté.
Per exemple, si tens aquesta matriu:
a = np.array([1, 2, 3, 4, 5, 6])I poses el mètode a? et surt:
a?Type: ndarrayString form: [1 2 3 4 5 6]Length: 6File: ~/anaconda3/lib/python3.9/site-packages/numpy/__init__.pyDocstring: <no docstring>Class docstring:ndarray(shape, dtype=float, buffer=None, offset=0, strides=None, order=None)Guardar y recuperar matrius NumPy en fitxers
La secció descriu: np.save, np.savez, np.savetxt, np.load, np.loadtxt
És important guardar i carregar seves matrius al disc sense haver de tornar a executar el codi. Afortunadament, hi ha diverses maneres de salvar i carregar objectes amb NumPy.
Els objectes ndarray es poden guardar i carregar dels fitxers de disc amb loadtxt i savetxt, si són fitxers de text pla; load i save si són funcions que manejen fitxers binaris de NumPy.
És fàcil de guardar i carregar i array amb np.save() i np.load() en el format npy.
a = np.array([1, 2, 3, 4, 5, 6])np.save('filename', a)b = np.load('filename.npy')print(b)[1 2 3 4 5 6]Però aquesta forma apenes s’utilitza i el més habitual és llegir i guardar una matriu de NumPy com un arxiu de text pla amb un archiu .csv o .txt amb np.savetxt i recuperar-lo amb np.loadtxt.
csv_arr = np.array([1, 2, 3, 4, 5, 6, 7, 8])np.savetxt('new_file.csv', csv_arr)np.loadtxt('new_file.csv')array([1., 2., 3., 4., 5., 6., 7., 8.])Aquestes funcions accepten paràmetres opcionals com:
- delimitador (pot ser un símbol com el ; la , el tabulador o un altre)
- header primera linia del fitxer, que no es posarà a l’array
- usecols et permet dir quines columnes vols llegir.
Importació y exportació de un CSV amb Pandas.
Es fàcil de llegir un CSV que conté informació rellevant que volguem inserir en un array (que sigui homogènia, és clar)
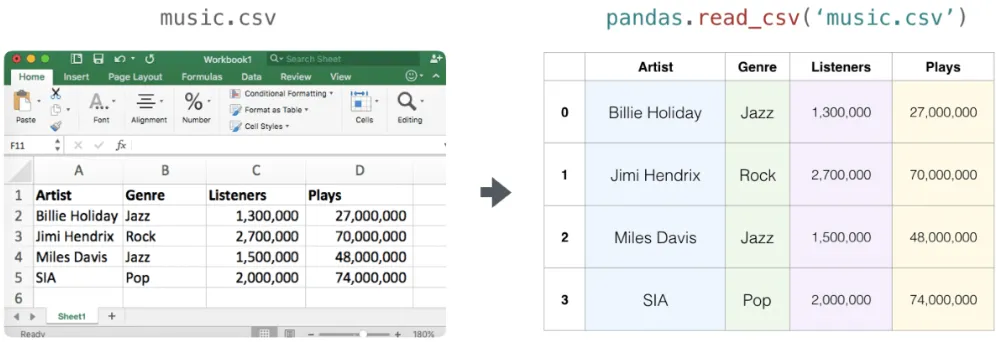
La forma més fácil i convenient de fer-ho és amb la llibreria Pandas.
Si ja tens ganes de veure Pandas en produnditat, accedeix a la nostra guia de Pandas
Un cop fet, ja pots crear el teu fitxer .py i cercar (o crear) un fitxer en format CSV per provar:
Billie Holiday;Jazz;1300000;27000000Jimmie Hendrix;Rock;2700000;70000000Miles;Davis;Jazz;1500000;48000000SIA;Pop;2000000;74000000import pandas as pd# If all of your columns are the same type:x = pd.read_csv('music.csv', header=0).valuesprint(x)[['Billie Holiday' 'Jazz' 1300000 27000000] ['Jimmie Hendrix' 'Rock' 2700000 70000000] ['Miles Davis' 'Jazz' 1500000 48000000] ['SIA' 'Pop' 2000000 74000000]]Si en comptes de tot el fitxer, només vols seleccionar algunes columnes ho pots fer amb el paràmetre usecols.
x = pd.read_csv('music.csv', usecols=['Artist', 'Plays']).valuesprint(x)[['Billie Holiday' 27000000] ['Jimmie Hendrix' 70000000] ['Miles Davis' 48000000] ['SIA' 74000000]]És fàcil d’usar Pandas per tal d’exportar la matriu. Ho pots fer transformant la matriu a DataFrame, la estructura de Pandas per gestionar dades tabulars.
Un cop fet, pots usar el mètode de Pandas to_csv
a = np.array([[-2.58289208, 0.43014843, -1.24082018, 1.59572603], [ 0.99027828, 1.17150989, 0.94125714, -0.14692469], [ 0.76989341, 0.81299683, -0.95068423, 0.11769564], [ 0.20484034, 0.34784527, 1.96979195, 0.51992837]])df = pd.DataFrame(a)print(df)df.to_csv('pd.csv') 0 1 2 30 -2.582892 0.430148 -1.240820 1.5957261 0.990278 1.171510 0.941257 -0.1469252 0.769893 0.812997 -0.950684 0.1176963 0.204840 0.347845 1.969792 0.519928Pots recuerar el contingut del fitxer:
data = pd.read_csv('pd.csv')L’altra opció és guardar la matriu dirèctament:
np.savetxt('np.csv', a, fmt='%.2f', delimiter=',', header='1, 2, 3, 4')Si estàs usant la línea de comandes de Linux, pots llegir el teu CSV guardat en sense obrir-lo amb la comanda cat:
$ cat np.csv1, 2, 3, 4-2.58,0.43,-1.24,1.600.99,1.17,0.94,-0.150.77,0.81,-0.95,0.120.20,0.35,1.97,0.52O pots obrir-lo amb qualsevol editor.
Exercici lectura fitxer CSV.
Importa en un array bidimensional de Numpy un fitxer CSV de temperatures mensuals de Barcelona els últims 10 anys.
Després de tractar-lo, el fitxer CSV té el següent contingut:
Any,Temp_Mitjana_Gener,Temp_Mitjana_Febrer,Temp_Mitjana_Marc,Temp_Mitjana_Abril,Temp_Mitjana_Maig,Temp_Mitjana_Juny,Temp_Mitjana_Juliol,Temp_Mitjana_Agost,Temp_Mitjana_Setembre,Temp_Mitjana_Octubre,Temp_Mitjana_Novembre,Temp_Mitjana_Desembre2014,9.8,10.1,12.3,15.3,16.2,21.7,22.6,23,22,19.6,13.6,9.12015,9.1,8.2,12,14.8,19.1,23.2,26.0,23.50,19.7,16.7,14.3,12.62016,10.7,11.3,11.1,13.6,16.4,21.6,24.9,24.5,22.3,17.1,12.7,11.52017,7.9,11.4,13.3,14.2,18.3,23.6,24.2,24.5,19.5,18.6,12.5,8.52018,10.5,6.7,10.8,14.7,17.1,21.5,25.3,25.8,22.5,17.0,12.4,11.12019,8.1,11.9,13.5,13.4,15.6,21.9,25.4,25.1,21.8,18.5,11.9,11.22020,10.0,12.8,11.9,14.3,19.4,20.1,25.0,25.5,21.7,16.4,14.7,9.32021,7.7,11.6,12.1,12.9,17.3,23.3,24.8,24.5,23.0,18.1,11.3,10.92022,10.2,11.8,10.8,14.1,20.7,24.7,26.7,27.2,22.5,20.7,15.2,12.62023,9.2,10.3,14.1,16.1,18.1,23.4,25.5,26,23.2,20.2,14.8,12.1Per començar, el guardem amb el nom temperaturesbcn_2014_2023.csv
Realitza 3 operacions estadístiques agrupades que consideris rellevants sobre l’array.
Millores: El contingut original del fitxer CSV de temperatures l’hem obtingut de portal de dades obertes de l’Observatori Fabra i Puig de Barcelona, que recopila les temperatures des del 1780. Aconsegueix que el programa descarregui automàticament el fitxer si no existeix al disc.
{% sol %}
Per llegir el fitxer CSV i posar-lo en un array de Numpy, ometent la primera columna i la primera fila, podem utilitzar la funció np.loadtxt amb els paràmetres adequats per saltar la primera fila i ometre la primera columna.
Aquest codi fa les següents operacions:
- Utilitza
np.genfromtxtper llegir el fitxer CSV i convertir-lo a array. - El paràmetre
delimiter=’,’ especifica que els valors estan separats per comes. - El paràmetre
skip_header=1 fa que es salti la primera fila del CSV (les capçaleres). - El paràmetre
usecols=range(1, 13) fa que es llegeixin només les columnes de la 1 a la 12 (les temperatures de Gener a Desembre, ometent la primera columna que és l’any).
import numpy as npimport urllib3import os.path
def get_file(url, file): http = urllib3.PoolManager() if not os.path.isfile(file): response = http.request("GET", url)
# Comprovar si la petició ha estat exitosa if response.status == 200: print(f"Descarregant el fitxer: {file}") with open(file, "wb") as f: f.write(response.data) else: print(f"Error en descarregar el fitxer: {response.status}")
return file
def read_csv(file): # Llegir el fitxer CSV i ometre la primera fila i primera columna data = np.loadtxt(file, delimiter=',', skiprows=1, usecols=range(1, 13)) # Llegim els anys, si els necessitem (no és el cas) # years = np.loadtxt(file, delimiter=',', skiprows=1, usecols=range(0, 1), dtype='int16') # print(years) return data
def mitjana_ultims_anys(data,n_ultims_anys = 10): # Selecciona dades dels últims anys (n_ultims_anys) opcionalment. data_ultims_anys = data[-n_ultims_anys:] # print(data_ultims_anys) mitjana_ultims_anys = np.mean(data_ultims_anys, axis=1) print(f"Mitjana temperatures mensuals últims {n_ultims_anys} anys: \n") print(mitjana_ultims_anys)
def max_min(data,n_ultims_anys = 10): # Selecciona dades dels últims anys (n_ultims_anys) opcionalment. data_ultims_anys = data[-n_ultims_anys:] max_per_any = np.max(data_ultims_anys, axis=1) min_per_any = np.min(data_ultims_anys, axis=1) print(f"Temperatura màxima últims {n_ultims_anys} anys: {max_per_any}") print(f"Temperatura mínima últims {n_ultims_anys} anys: {min_per_any}")
url = "https://opendata-ajuntament.barcelona.cat/data/dataset/73f09843-ab4e-4f13-81fb-b801ca371909/resource/0e3b6840-7dff-4731-a556-44fac28a7873/download/temperaturesbcndesde1780_2023.csv"file = "temperaturesbcndesde1780_2023.csv"
file = get_file(url, file)data = read_csv(file)
mitjana_ultims_anys(data)max_min(data,20)
# mitjana_per_mes = np.mean(data, axis=0)# print("\nMitjana de la temperatura de cada mes al llarg dels anys:")# print(mitjana_per_mes){% endsol %}