L'estadística ens permet extreure dades d'un conjunt enorme de dades de tal manera que ens permeten entendre les relacions entre les dades.
On this page
Introducció
…
Conceptes
Els estadístics són indicadors
Els valors estadístics només tenen sentit quan s’apliquen a un grup gran de dades, poques vegades en l’àmbit individual.
Per exemple, l’altura mitjana dels homes a Espanya és de 176 centímetres i el de les dones de 162 centímetres.
Quants en aquesta classe mesureu exactament aquesta altura?
Però la majoria us aproximeu a aquest valor.
Tipus de dades
Hi ha dades de diversos tipus.
Les dades quantitatives són dades numèriques que es poden mesurar, com pot ser el pes, l’edat o alçada.
Les dades qualitatives es tenen o no, per exemple el color dels ulls, la nacionalitat.
Mesures de tendència central
Els tres indicadors bàsics són la mitjana, la mediana i la moda.
Mitjana
La mitjana és un indicador que només es pot utilitzar amb dades quantitatives.
Consisteix a sumar totes les dades i dividir el resultat entre el nombre total d’elements.
Calcula la mitjana d’aquesta llista: [3, 8, 10, 13, 16, 18]
data = [3, 8, 10, 13, 16, 18]
mean = sum(data) / len(data)print(f"Mean of the data: {mean:.2f}")Python és un llenguatge pensant per enginyers i científics.
Per tant, a diferència d’altres llenguatges incorpora per defecte una llibreria d’estadística.
Pots calcular directament la mitjana de les dades anteriors amb statistics.
data = [3, 8, 10, 13, 16, 18]
mean = statistics.mean(data)
print(f"Mean of the data: {mean:.2f}")Moda
La moda és el valor que apareix més sovint.
En aquesta llista, quin és el valor que apareix més sovint?
data = [3, 8, 3, 7, 7, 10, 13, 7, 1, 6]És el 7
En aquest cas és més fàcil fer l’exercici a mà que escriure un codi en Python per a calcular la moda. 👻
Amb statistics podem calcular fàcilment la moda d’un conjunt de dades:
import statistics
data = [7, 3, 9, 1, 8, 2, 5, 6, 4, 5, 9, 2, 8, 1, 7, 3, 5, 4, 6, 9, 2, 5, 1, 8, 3, 7, 6, 4, 9, 2, 5, 1, 8, 3, 7, 6, 4, 9, 2, 5, 5, 1, 8, 3, 7, 6, 4, 9, 2, 5, 1, 8]
mode = statistics.multimode(data)assert mode == [5] , f"result is {mode}"Pots observar que el resultat és una llista.
El motiu és que dos o més valors poden apareixen el mateix nombre de vegades.
import statistics
data = [8, 7, 8, 7, 3]
mode = statistics.multimode(data)assert mode == [8, 7], f"result is {mode}"Mediana
La mediana és el valor que està al mig d’un conjunt de dades ordenades.
data = [8, 7, 8, 7, 3]
data.sort()median = data[2]
assert median == 7, f"result is {median}"Exemple
A continuació tens el salari mensual de 5 treballadors d’un pas no tan imaginari:
data = [800, 1000, 1000, 4_000, 5_000, 50_000, 300_000]Calcula la mitja, la moda i la mitjana:
import statistics
data = [800, 1000, 1000, 4_000, 5_000, 50_000, 300_000]
assert int(statistics.mean(data)) == 51685assert statistics.median(data) == 4000assert statistics.mode(data) == 1000Dibuixa un gràfic de barres de les dades:
Aquest pais podria ser els Estats Units, per exemple.
És un pais on el PIB per capita és dels més alts del món, on el seu mig és molt bo, on el ciutadà mig té un bon sou, però on una bona part de la població viu en la pobresa.
Pots veure que depen el conjunt de dades cada indicador explica una història diferent.
🤔
Exemple
Tenim les notes de 4 alumnes en 3 examens en un DataFrame. Seran números enters.
import altair as altimport polars as plimport streamlit as st
df = pl.DataFrame({ 'alumne': ['Anna', 'Bernat', 'Carla', 'David'], 'examen-1': [7, 4, 10, 6], 'examen-2': [6, 8, 7, 9], 'examen-3': [8, 7, 9, 8]})
df = df.with_columns( pl.mean_horizontal([pl.col('examen-1'), pl.col('examen-2'), pl.col('examen-3')]).alias('mitjana'))
chart = alt.Chart(df).mark_bar().encode( x="mitjana", y="alumne")
st.altair_chart(chart)Mesures de dispersió
Les mesures de dispersió descriuen com varien les dades respecte al seu centre.
TODO: Pendent de revisar completament a partir d’aquí
[Box Plot]((https://altair-viz.github.io/user_guide/marks/boxplot.html)
Rang
Rang: El rang és la diferència entre l’observació més alta (màxim) i la més baixa (mínim).
Rang = | Màx - Mín |
Desviació respecte a la mitjana: La desviació respecte a la mitjana és la diferència en valor absolut entre cada valor de la variable estadística i la mitjana aritmètica. La suma de les desviacions respecte de la mitjana és zero. Aquest càlcul es fa per a calcular el pendent de les rectes de regressió.
Quantil: Els quantils són punts presos a intervals regulars de la funció de distribució d’una variable aleatòria. Les mostres s’ordenen segons els valors de menor a major, i el quantil és el valor en aquest punt.
Si el punt es pren en tant per cent de les observacions, s’anomenen percentil. Si les observacions es divideixen en quatre quarts, les tres divisions es diuen quartils (Q1=25%, Q2=50%, Q3=75%). Q2 és la Mediana. També hi ha decils (D1=10%, … D9=90%) si volem filar més prim.
L’aplicació pràctica que haureu vist dels quantils és ordenar les publicacions científiques per H-Index, on les del Q1 són les més recomanades.
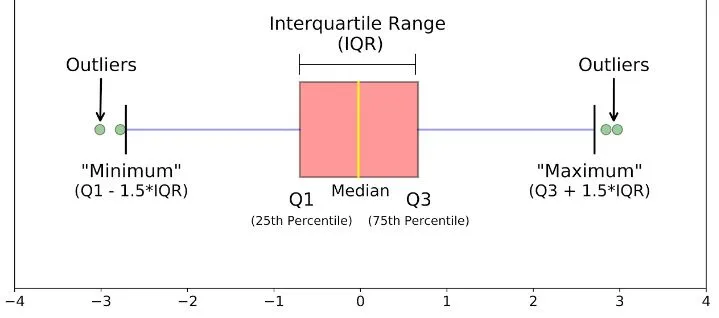
Rang interquartílic:
És la diferència (resta) entre el primer i el tercer quartil.
IQR = Q3 − Q1.
Com mostrar estadístiques descriptives ?
Molt senzill! Pandas proporciona una funció que ja hem vist des del primer dia: describe.
Les que aquesta funció no proporcioni (com la moda) són senzilles de calcular.
Provem-ho amb el dataset dels examens dels alumnes; amb 4 alumnes nous.
import pandas as pdimport numpy as np
data1 = { 'Alumne': ['Anna', 'Bernat', 'Carla', 'David'], 'Examen1': [7, 4, 10, 6], 'Examen2': [6, 8, 7, 9], 'Examen3': [8, 7, 9, 8]}data2 = { 'Alumne': ['Wally', 'Xavi', 'Yaiza', 'Zulema'], 'Examen1': [5, 6, 10, 6], 'Examen2': [3, 8, 7, 8], 'Examen3': [6, 7, 8, 10]}df1 = pd.DataFrame(data1)df2 = pd.DataFrame(data2)df_total = pd.concat([df1, df2], ignore_index=True)print(df_total.describe())print(df_total['Examen1'].describe())Resultat:
Examen1 Examen2 Examen3count 8.000000 8.00000 8.000000mean 6.750000 7.00000 7.875000std 2.187628 1.85164 1.246423min 4.000000 3.00000 6.00000025% 5.750000 6.75000 7.00000050% 6.000000 7.50000 8.00000075% 7.750000 8.00000 8.250000max 10.000000 9.00000 10.000000count 8.000000mean 6.750000std 2.187628min 4.00000025% 5.75000050% 6.00000075% 7.750000max 10.000000Fixeu-vos totes les estadístiques que hem aconseguit:
- count: Recompte de files/elements
- Mean: Mitjana aritmètica
- std: Desviació típica
- max i min: Màxim i mínim
- 50%: Mediana
- 25% i 75%: Quartil1 i Quartil3
Estadístiques generals, i també de tots els examens individualemnt (fa estadístiques de totes les dades numèriques).
Per calcular l’IQR, també ho tenim molt fàcil:
iqr = df['Examen1'].quantile(0.75) - df['Examen1'].quantile(0.25)print(iqr)El resultat és 7.75 - 5.75 = 2
1.- Estadístiques d’un institut.
Donat el dataframe de les notes dels 8 alumnes; realitza el següent.
- Mostra totes les estadístiques de les notes de l’examen 3.
- Mostra totes les notes de l’Anna i la Yaiza.
- Calcula l’IQR de les notes de la columna
Examen1. - Crea una columna anomenada
Finalamb lamitjana aritmètica dels 3 examens. - Mostra la mitjana aritmètica i desviació típica de tots els examens (columna
Final)
Assegura’t que el codi passi els tests que hem posat al final de tot.
import pandas as pdimport numpy as np
data = { 'Alumne': ['Anna', 'Bernat', 'Carla', 'David', 'Wally', 'Xavi', 'Yaiza', 'Zulema'], 'Examen1': [7, 4, 10, 6, 5, 6, 10, 7], 'Examen2': [6, 8, 7, 9, 3, 8, 7, 8], 'Examen3': [8, 7, 9, 8, 6, 7, 8, 10]}df1 = pd.DataFrame(data)
#El teu codi va aquí
# Testsassert IQR == 2, "Error: IQR incorrecte."assert df1['Final'].iloc[0] == 7, "Error: Nota Final incorrecte per Anna."assert round(mean_final, 2) == 7.25, "Error: Mitjana incorrecta."assert round(std_final, 2) == 1.32, "Error: Desviació típica incorrecta."Valors indefinits: nan.
I què passaria si algú no fes l’examen en l’exemple anterior ? Com calcularia la mitjana ?
I si després el fes, com substituïriem la nota ?
Primer, ho representem amb el valor Nan, que es defineix així: np.nan.
import numpy as np
# Afegir un nou alumne amb np.nannou_alumne = pd.DataFrame({ 'Alumne': ['Marc'], 'Examen1': [np.nan], 'Examen2': [6], 'Examen3': [7]})df1 = pd.concat([df1, nou_alumne], ignore_index=True)
# Calcular la mitjana per a Marc (actualment amb np.nan)mitjana_alumne = df1.loc[df1['Alumne'] == 'Marc', ['Examen1', 'Examen2', 'Examen3']].mean(axis=1)print(f"Mitjana aritmètica de Marc (amb np.nan)= {mitjana_alumne.iloc[0]}")
# Reemplaçar np.nan per un 8df1.loc[df1['Alumne'] == 'Marc', 'Examen1'] = 8
# Tornar a calcular la mitjana per a Marcnova_mitjana_alumne = df1.loc[df1['Alumne'] == 'Marc', ['Examen1', 'Examen2', 'Examen3']].mean(axis=1)print(f"Mitjana aritmètica de Marc (sense np.nan)= {nova_mitjana_alumne.iloc[0]}")Com podem veure, per a realitzar operacions estadístiques pandas ignora els nan i només té en compte els valors existents.
Però per operacions matemàtiques si que és necessari ometre o reemplaçar per números els np.nan.
Valors atípics (outlier).
Un valor atípic (outlier) és una observació que difereix tan àmpliament de la resta de dades que podem pensar que s’ha comès un error.
Concretament, un valor outlier serà:
-
Un valor inferior al
quartil1 - 1,5 * IQR -
Un valor superior al
quartil3 + 1,5 * IQR
Recordm que l’IQR és el rang interquartílic: q3 - q1.
Sempre cal considerar-ne la causa. Si són causats per errors en la lectura de les dades o mesures inusuals s’esborren, però si no cal considerar-les.
Pandas és una molt bona llibreria, però encara no ha previst com calcular els outliers.
De tota manera, amb aquest senzill codi podrem trobar-los i eliminar-los.
Si només volem trobar-los, ens oblidem del loc.
def remove_outliers(df_in, col_name): q1 = df_in[col_name].quantile(0.25) q3 = df_in[col_name].quantile(0.75) iqr = q3-q1 #Interquartile range fence_low = q1-1.5*iqr fence_high = q3+1.5*iqr df_out = df_in.loc[(df_in[col_name] > fence_low) & (df_in[col_name] < fence_high)] return df_out- Boxplot: Un boxplot és una gràfica que mostra diversos descriptors alhora d’una o més variables: Els
tres quartils,el "mínim" i "màxim" calculatsi elsoutliers. Són usats en molts àmbits.
Les llibreries com Seaborn o Matplotlib els generen molt fàcilment.
2.- Estadístiques de dispersió i outliers
Ens han donat un dataframe amb la edat, altura, pressió sistòlica i diastòlica de diversos pacients.
La pressió arterial normal, en el cas de la majoria dels adults, es defineix com una pressió sistòlica de menys de 120 i una pressió diastòlica de menys de 80.
Doncs bé, ens demanen mostrar estadístiques centrals i de dispersió de totes les variables, calcular l’amplitud interquartilica de les pressions i crear un nou dataframe sense els outliers de la pressió (sigui sis o dia).
Codi de partida:
df_pacients = pd.DataFrame({ 'edat' : [50,43,22,61,64,54,38,98], 'altura' : [1.75,1.57,1.6,1.66,1.63,1.79,1.70,1.61], 'pr_sis' : [125,105,150,800,130,114,105,119], 'pr_dia' : [81,74,84,76,80,78,69,81]})
# Tractament dels outliersSolució esperada:
edat altura pr_sis pr_dia0 50 1.75 125 811 43 1.57 105 742 22 1.60 150 844 64 1.63 130 805 54 1.79 114 786 38 1.70 105 697 98 1.61 119 81 edat altura pr_sis pr_diacount 7.000000 7.000000 7.000000 7.000000mean 52.714286 1.664286 121.142857 78.142857std 23.949351 0.083238 15.826440 5.080307min 22.000000 1.570000 105.000000 69.00000025% 40.500000 1.605000 109.500000 76.00000050% 50.000000 1.630000 119.000000 80.00000075% 59.000000 1.725000 127.500000 81.000000max 98.000000 1.790000 150.000000 84.000000def iqr(df_in, col_name): ''' Calcula l'amplitud interquartilica (-1,5*iqr,+1,5*iqr) i retorna els valors inferior i superior. ''' q1 = df_in[col_name].quantile(0.25) q3 = df_in[col_name].quantile(0.75) iqr = q3-q1 #Interquartile range fence_low = q1-1.5*iqr fence_high = q3+1.5*iqr # Si, es poden retornar 2 valors. return fence_low, fence_high
def remove_outliers(df_in, col_name): ''' Esborra valors outliers (-1,5*iqr,+1,5*iqr) d'una columna d'un dataframe. ''' fence_low, fence_high = iqr(df_in,col_name) df_out = df_in.loc[(df_in[col_name] > fence_low) & (df_in[col_name] < fence_high)] return df_out
df_pacients = pd.DataFrame({ 'edat' : [50,43,22,61,64,54,38,98], 'altura' : [1.75,1.57,1.6,1.66,1.63,1.79,1.70,1.61], 'pr_sis' : [125,105,150,800,130,114,105,119], 'pr_dia' : [81,74,84,76,80,78,69,81]})
print('IQR pr_sis',iqr(df_pacients,'pr_sis'))print('IQR pr_dia',iqr(df_pacients,'pr_dia'))# la edat també té un iqr, però no l'esborrem perquè no passa res per# tenir pacients grans.# print('IQR edat',iqr(df_pacients,'edat'))
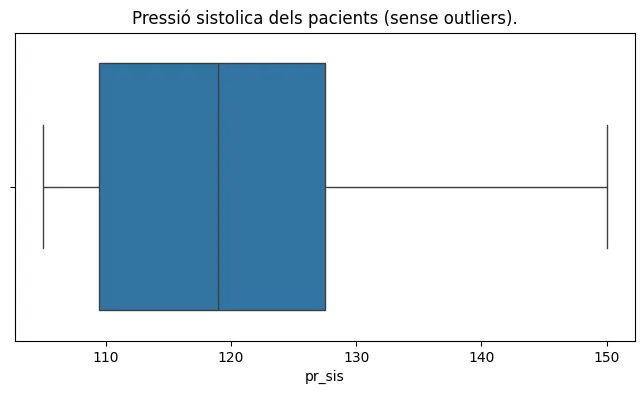
df_pacients_clean = remove_outliers(df_pacients,'pr_sis')print(df_pacients_clean)print(df_pacients_clean.describe())Creació de boxplot per estudiar els quartils de variables amb Seaborn.
Anem a crear gràfics de boxplot sobre l’exemple anterior dels pacients, concretament per a la pressió sistòlica.
Ho podem fer amb Matplotlib, però serà més senzill usar la llibreria de gràfics Seaborn. Cal importar-la amb la comanda:
poetry add seabornEn el codi que hem usat abans, hem d’afegir la creació de 2 boxplot, un amb els outliers i l’altre sense els outliers (que podem esborrar amb la funció remove_outliers)
import pandas as pdimport numpy as npimport seaborn as sns
def iqr(df_in, col_name): ''' Calcula l'amplitud interquartilica (-1,5*iqr,+1,5*iqr) i retorna els valors inferior i superior. ''' q1 = df_in[col_name].quantile(0.25) q3 = df_in[col_name].quantile(0.75) iqr = q3-q1 #Interquartile range fence_low = q1-1.5*iqr fence_high = q3+1.5*iqr # Si, es poden retornar 2 valors. return fence_low, fence_high
def remove_outliers(df_in, col_name): ''' Esborra valors outliers (-1,5*iqr,+1,5*iqr) d'una columna d'un dataframe. ''' fence_low, fence_high = iqr(df_in,col_name) df_out = df_in.loc[(df_in[col_name] > fence_low) & (df_in[col_name] < fence_high)] return df_out
df_pacients = pd.DataFrame({ 'edat' : [50,43,22,61,64,54,38,98], 'altura' : [1.75,1.57,1.6,1.66,1.63,1.79,1.70,1.61], 'pr_sis' : [125,105,150,800,130,114,105,119], 'pr_dia' : [81,74,84,76,80,78,69,81]})
#print(df_pacients.describe())print('IQR pr_sis',iqr(df_pacients,'pr_sis'))print('IQR pr_dia',iqr(df_pacients,'pr_dia'))# la edat també té un iqr, però no l'esborrem perquè no passa res per# tenir pacients grans.# print('IQR edat',iqr(df_pacients,'edat'))
plt.figure(figsize=(8, 4))plt.title('Pressió sistolica dels pacients (amb outliers).')sns.boxplot(data=df_pacients, x="pr_sis")plt.show()
df_pacients_clean = remove_outliers(df_pacients,'pr_sis')print(df_pacients_clean)print(df_pacients_clean.describe())
plt.figure(figsize=(8, 4))plt.title('Pressió sistolica dels pacients (sense outliers).')sns.boxplot(data=df_pacients_clean, x="pr_sis")plt.show()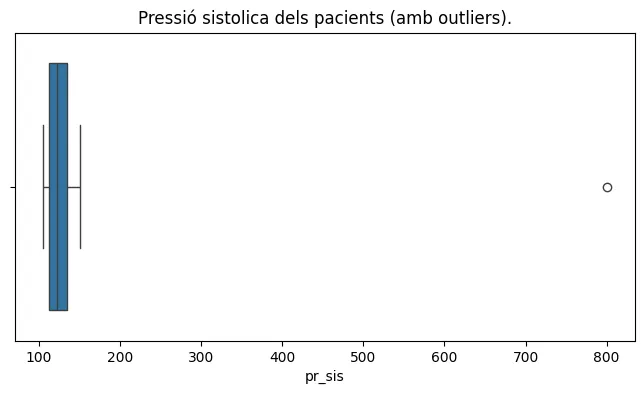
Fixeu-vos amb la sintaxis bàsica del gràfic boxplot de Seaborn:
- data Admet DataFrames, Series, dict, array, or list of arrays.
- x Variable que ens interessa (si a data hi ha DataFrame)
- y Si volem crear diversos plotbox classificats per un camp categòric com el gènere (si a data hi ha DataFrame)
- hue Si volem classificar encara més els boxplots.
Per tant, podem generar diversos plotbox d’una mateixa variable, classificats en camps categòrics (per exemple, un plotbox per homes i un altre per dones).
Ho podreu veure amb un exemple sobre un dels datasets més coneguts del món, el dels passatgers del Titanic, que té un munt de carecterístiques de cadascun
No ens caldrà descarregar-lo perquè Seaborn ja incorpora uns quants dataSets descarregats que podem importar fàcilment a un dataFrame.
import pandas as pdimport numpy as npimport matplotlib.pyplot as pltimport seaborn as sns
titanic_df = sns.load_dataset("titanic")print(titanic_df.info())
sns.boxplot(data=titanic_df, x="age", y="class")plt.title("Distribució edats passatgers/es del Titanic en funció del tipus de bitllet")plt.show()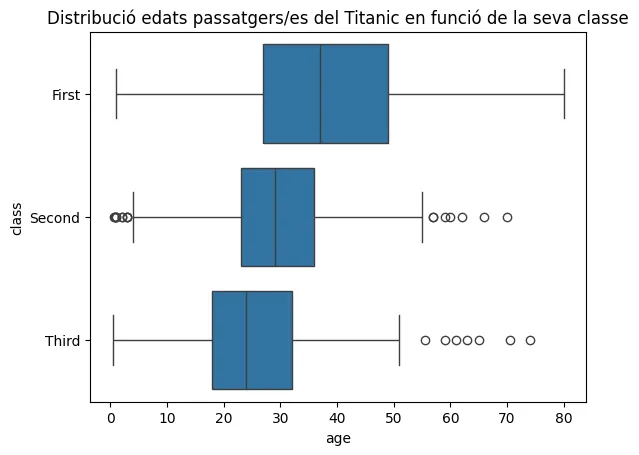
Fixeu-vos! Amb només dues linies noves ho hem aconseguit :)
Recompte de variables agrupat per categories amb Seaborn.
Partint del mateix exemple dels passatgers del Titanic i Seaborn; imaginem-nos que volem saber el número de passatgers homes i dones de cada classe.
Com ho fem ? Amb el gràfic de Seaborn catplot, que genera diagrames de barres classificables per diversos criteris (la x i el hue) i que permet fer operacions automàtiques dins del grup amb el paràmetre kind.
# Now let separate the gender by classes passing 'Sex' to the 'hue' parametersns.catplot(x='class', data=titanic_df, hue='sex', kind='count')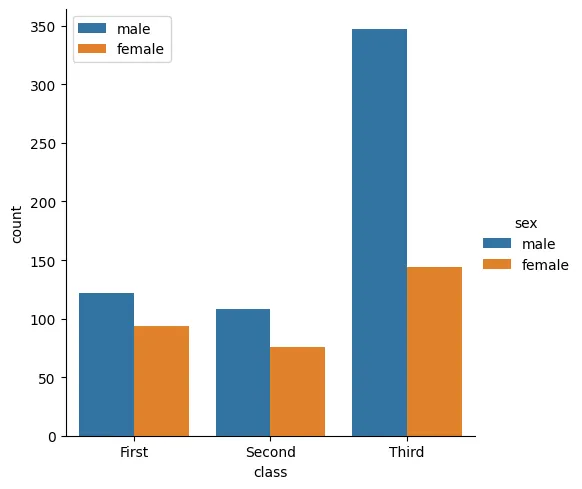
Teniu més d’exemples d’ús de catplot a la web de Seaborn
3.- Crea un gràfic que que mostri quants superivents hi ha hagut de cada classe de bitllet (First,Second,Third)
sns.catplot(x='alive', data=titanic_df, hue='class', kind='count')Distribució normal
La naturalesa no és una fábrica amb un procés industrial que fabrica components d’alta qualitat tots exactament iguals.
Més aviat són elements fets a mà en què la majoria s’assemblen, però en cap cas tots són iguals.
Una de les distribucions teòriques més utilitzada a la pràctica és la distribució normal, també anomenada distribució gaussiana en honor al matemàtic Carl Friedrich Gauss.
Charles Darwin i el seu cosí Francis Galton van descobrir que les variables associades a fenòmens naturals i quotidians que experimenten totes les espècies (inclòs l’ésser humà) segueixen, aproximadament una distribució normal.
Distribució normal vol dir que la majoria dels subjectes segueixen més o menys el que és la norma respecte a aquella dada.
Per exemple, si la norma és que l’alçada dels espanyols és de 176 centímetres una gran majoria més o menys ho són.
Forma i propietats distribució normal.
- La mitjana, la moda i la mediana són iguals.
- L’àrea total sota la corba és igual a 1.
- La corba és simètrica al voltant de la mitjana.
- És ideal per a representar variables numèriques contínues (com la alçada, la edat de persones…)
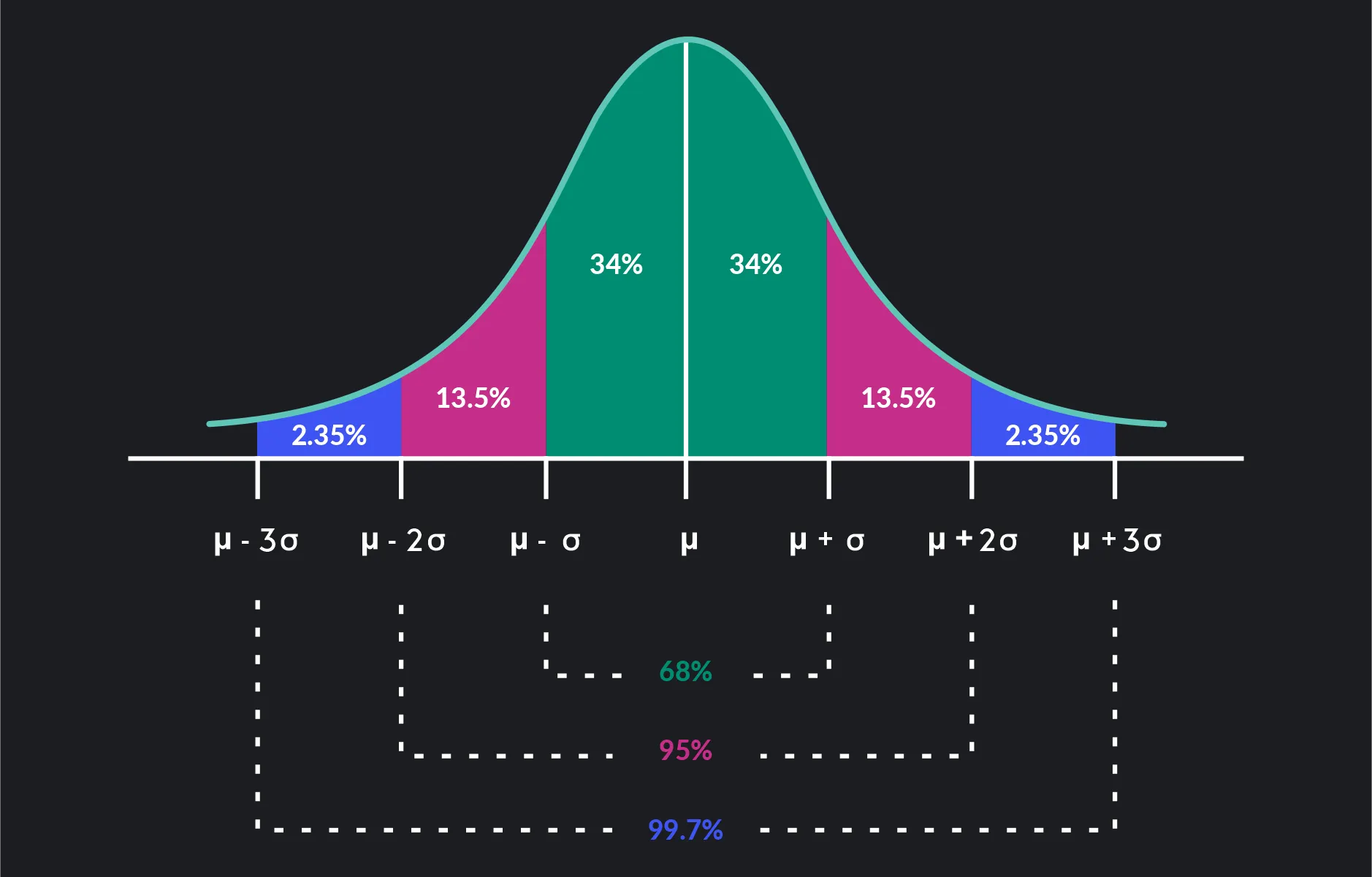
D’aquesta corba podem deduïr els següents intèrvals de confiança (IC):
- El 68% aprox. de les dades es troben dins d’una desviació estàndard de la mitjana.
- El 95% aprox. de les dades es troben dins de dues desviacions estàndard de la mitjana.
- El 99,7% aprox. de les dades es troben dins de tres desviacions estàndard de la mitjana.
I per a què ens serveixen aquestes propietats ?
Si volem estudiar probabilitats, ens va bé per deduïr que hi ha un 2,38% de probabilitats (aprox) que un esportista tingui una alçada superior a la mitjana + desviació típica multiplicada per 2.
Ho pots entendre millor veient la corba de distribució:
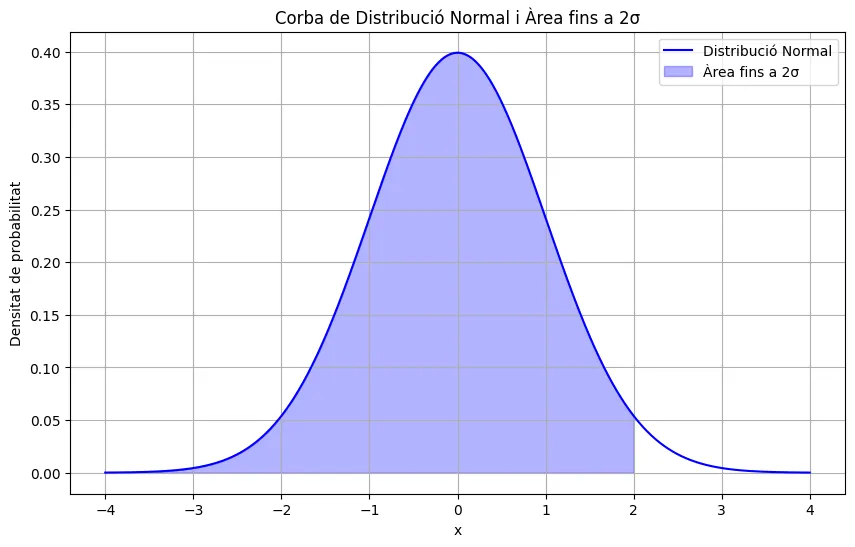
Si tens curiositat com hem creat la corba, aquí tens el codi:
import numpy as npimport matplotlib.pyplot as pltfrom scipy.stats import norm
# Càlcul del percentatge dins de +2 sigmamu = 0sigma = 1percent_within_2sigma = norm.cdf(mu + 2*sigma, mu, sigma) * 100print(f"Percentatge des de l'inici fins al +2σ: {percent_within_2sigma:.2f}%")
# Dibuixar una corba de distribució normal estàndardx = np.linspace(-4, 4, 1000) # Valors de x des de -4 fins a 4y = norm.pdf(x, 0, 1) # Funció de densitat de probabilitat per a una normal estàndard
# Àrea sota la corba des de l'inici fins a 2 sigmax_fill = np.linspace(-4, 2, 1000)y_fill = norm.pdf(x_fill, 0, 1)
plt.figure(figsize=(10, 6))plt.plot(x, y, 'b-', label='Distribució Normal')plt.fill_between(x_fill, y_fill, 0, alpha=0.3, color='b', label='Àrea fins a 2σ')
plt.title('Corba de Distribució Normal i Àrea fins a 2σ')plt.xlabel('x')plt.ylabel('Densitat de probabilitat')plt.legend()
plt.grid(True)plt.show()La segona distribució més comuna és la distribució binomial; que sol donar-se en obtenir mostres del clima (temperatures, pluges…) i també en esdeveniments on intervé l’atzar (l’aletorietat): probabilitat d’obtenir una cara d’un dau, una moneda…
Aprofundir en els tipus de distribucions en estadística queda fora de l’abast d’aquest tutorial.
De fet, ja ho vam veure a la sessió de Matplotlib
Exemple distribució normal.
Anem a veure com dibuixar un histograma i una corba d’una distribució Normal. que servirà per a comparar si la nostra mostra té una forma semblant a la corba normal.
Per aquest exemple usarem una funció molt útil de Numpy que genera dades que segueixin una distribució normal.
Veiem-ho amb un exemple fictici del nivell de colesterol a la sang de 300 pacients.
import numpy as npimport matplotlib.pyplot as plt
# Paràmetres per a la distribució normalmean = 200 # mitjana del colesterol (mg/dL)std_dev = 30 # desviació estàndard (mg/dL)n_samples = 300 # nombre de mostres
# Generar dades aleatòries amb una distribució normalcholesterol_levels = np.random.normal(mean, std_dev, n_samples)
# Crear l'histogramaplt.hist(cholesterol_levels, bins=20, density=True, alpha=0.6, color='g', edgecolor='black')
# Crear la corba de distribució normalxmin, xmax = plt.xlim()x = np.linspace(xmin, xmax, 100)p = np.exp(-0.5*((x-mean)/std_dev)**2) / (std_dev * np.sqrt(2 * np.pi))plt.plot(x, p, 'k', linewidth=2)
# Afegir títol i etiquetesplt.title('Distribució dels Nivells de Colesterol')plt.xlabel('Nivells de Colesterol (mg/dL)')plt.ylabel('Freqüència')
# Afegir línia vertical a la mitjanaplt.axvline(mean, color='b', linestyle='dashed', linewidth=2, label='Mitjana')
# Afegir línies verticals als intervals de confiança (±1 desviació estàndard)plt.axvline(mean - std_dev, color='r', linestyle='dotted', linewidth=2, label='-1 Desviació estàndard')plt.axvline(mean + std_dev, color='r', linestyle='dotted', linewidth=2, label='+1 Desviació estàndard')
plt.legend()plt.savefig('normald1.png')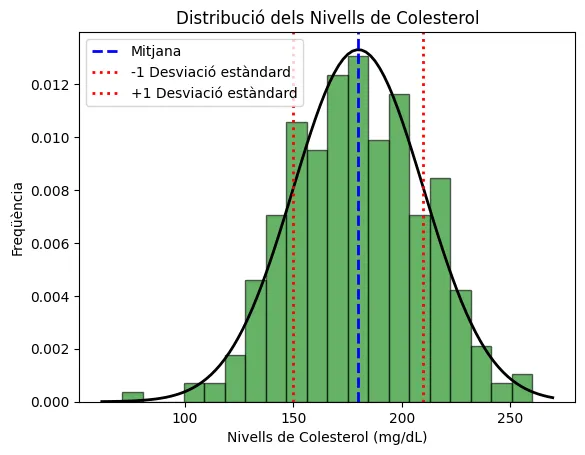
La sintaxis de la funció np.random.normal és:
- loc Mitjana aritmètica (mean) de la distribució.
- scale Desviació típica (std_dev) de la distribució. Ha de ser no negatiu.
- size Tamany (número d’elements) de la mostra
En quant a la sintaxi de plt.hist() remarquem el següent:
- data El més important, on li passem les dades.
- bins Matplotlib divideix els valors de la variable contínua en 20 intèrvals discrets, en 20 barres (bins=20).
- density Les àrees de les barres es normalitzen perquè la suma total sigui 1 (density=True).
- color Lletra per representar el color ‘g’ -> green.
- alpha Transparència del color del 60%.
- edgecolor Color de les vores.
Us animem a provar aquest diagrama, i a cercar altres exemples. És molt satisfactori realitzar aquest diagrama tan complet amb només 3 llibreries de Python i la comprensió de conceptes estadístics bàsics :)
Variància: La variància és la mitjana aritmètica del quadrat de les desviacions respecte a la mitjana d’una distribució estadística. La variància intenta descriure la dispersió de les dades. En resum, la variància seria la mitjana de les desviacions al quadrat. Es representa com σ2 (sigma minúscula al quadrat).
Desviació típica: La desviació típica és l’arrel quadrada de la variància. Es representa amb la lletra grega σ. En anglès es conèix com std = Standard Desviation.
Mesures de correlació
En moltes ocasions, ens pot interessar analitzar si ha una relació directa o inversa entre 2 variables d’una mostra.
Per exemple entre el temps i les temperatures, entre el pes i l’alçada de persones, l’edat i el nivell de sucre o el pes i el nivell de sucre.
Fins i tot, podem mostrar un mapa de correlacions, entre una variable i les altres variables (sempre i quan siguin quantitatives i del mateix tipus).
Anem a veure-ho amb un exemple senzill, el dataset tips; que conté dades de propines proporcionades per clients d’un bar, on tenim les dades de: preu del menjar(bill), gènere(sex), diners propina (tips), si és dinar o sopar(time), el número de persones(size), etc…
import pandas as pdimport seaborn as snsimport matplotlib.pyplot as plt
# Carregar el dataset de propinestips = sns.load_dataset("tips")
# Seleccionar només les variables numèriquesnumeric_tips = tips.select_dtypes(include='number')
# Calcular la matriu de correlaciócorr_matrix = numeric_tips.corr()
# Crear el heatmap de correlacióplt.figure(figsize=(10, 6))sns.heatmap(corr_matrix, annot=True, cmap='coolwarm', linewidths=0.5)plt.title('Heatmap de Correlació de Propines')plt.show()
# Crear el scatter plotplt.figure(figsize=(10, 6))sns.scatterplot(data=tips, x='total_bill', y='tip', hue='time')plt.title('Scatter Plot de Total Bill vs Tip')plt.xlabel('Total Bill')plt.ylabel('Tip')plt.legend(title='Time')plt.show()Fixeu-vos amb el mapa; com correlaciona totes les variables mumèriques: total_bill, tips, size:
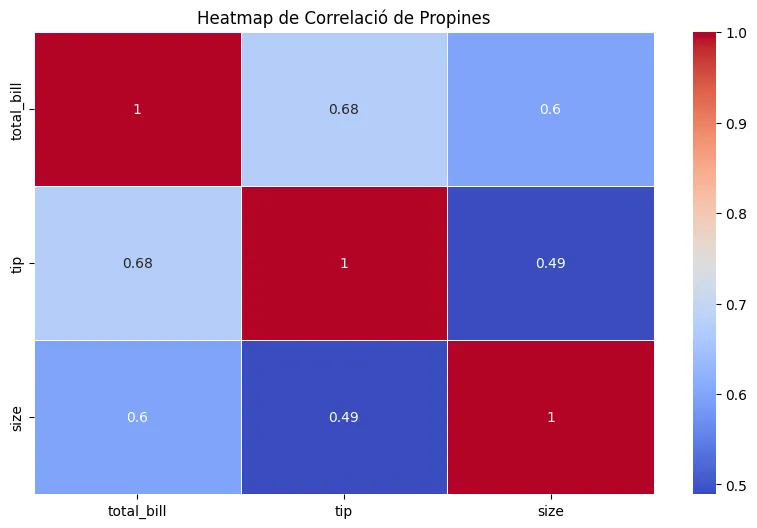
Podem observar una correlació directa:
- 0,68 entre el preu del menjar (total_bill) i els diners de propina (tips)
Diem que 2 variables estan fortament correlacionades directament si aquesta correlació és de 0,7 o superior, on el màxim és 1.
Per tant, en el nostre cas obtenim la informació que sovint (no sempre) es compleix com més val el que s’ha menjat més s’agraeix al servei en diners de propina superiors.
Finalment, comentar que hem dibuixat un altre gràfic de punts (scatterplot) que mira si hi ha correlació entre les propines i el preu del menjar, agrupat entre el temps de dinar i de sopar; perquè sempre va bé observar aquests gràfics per fer-nos una idea de la correlació de 2 variables a simple vista.
Seaborn també proporciona un altre tipus de gràfic molt potent per analitzar la distribució i correlació entre les variables, i fins i tot agrupar-les per una variabla categòrica (com poden ser ‘Time’, ‘Sex’ o ‘Smoker’).
import pandas as pdimport seaborn as snsimport matplotlib.pyplot as plt
tips = sns.load_dataset("tips")
# Crear el pairplot amb línies de millor ajustamentsns.pairplot(tips, kind='reg', hue='time', diag_kind='kde', markers=["o", "s"])plt.suptitle('Pairplot de Propines amb Línies de Millor Ajustament', y=1.02)plt.show()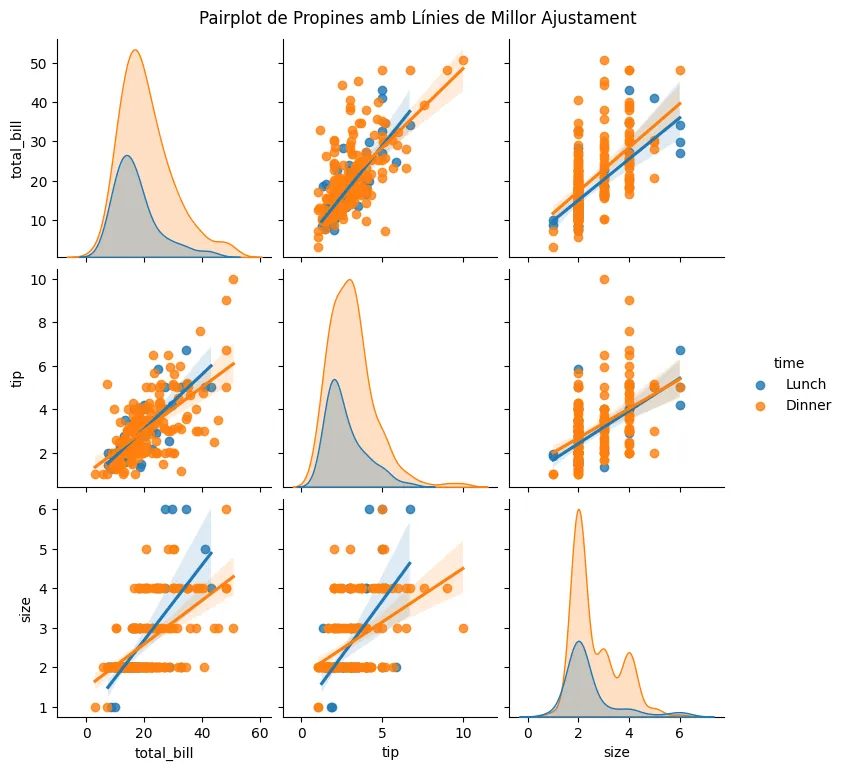
4.- Agafa el dataset dels pingüins de Palmer (també inclòs a Seaborn) i dibuixa la matriu de correlació entre totes les 4 variables numèriques. Comenta si has vist una forta correlació entre algún parell de variables.
Completa el codi per aconseguir-ho:
import pandas as pdimport seaborn as snsimport matplotlib.pyplot as pltdf = sns.load_dataset('penguins')numeric_peng = df.select_dtypes(include='number')matrix = numeric_peng.corr()sns.heatmap(matrix, annot=True, vmax=1, vmin=-1, center=0, cmap='vlag')plt.show()Hi ha una forta correlació entre la longitud de les aletes i el pes dels pingüins (de 0,87 sobre 1).